题目内容
已知向量
，
是两非零向量，在下列四个条件中，能使
，
共线的条件是
A．2
-3
=4
，
+2
=-3
B．存在相异实数λ，μ，使λ
+μ
=0
C．x
+y
=
（其中实数x，y满足x+y=0）
D．已知梯形ABCD中，
=
，
=
．
| a |
| b |
| a |
| b |
A．2
| a |
| b |
| e |
| a |
| b |
| e |
B．存在相异实数λ，μ，使λ
| a |
| b |
C．x
| a |
| b |
| 0 |
D．已知梯形ABCD中，
| AB |
| a |
| CD |
| b |
考点：命题的真假判断与应用,平行向量与共线向量
专题：平面向量及应用
分析：利用向量共线的条件判断A的正误，利用平面向量共线向量定理判断B的正误；利用共线向量定理判断C的正误；利用梯形形状判断D的正误；
解答：
解：对于A，∵向量
，
是两非零向量，2
-3
=4
，
+2
=-3
∴
=-
，
=-
，此时能使
，
共线，A正确；
对于B，存在相异实数λ，μ，使λ
+μ
=0，显然向量
，
是两非零向量是共线的，B正确；
对于C，x
+y
=
（其中实数x，y满足x+y=0）如果x=y=0则不能使
，
共线，C不正确；
对于D，已知梯形ABCD中，
=
，
=
．如果AB，CD是梯形的上下底，则正确，否则错误；
故答案为：AB．
| a |
| b |
| a |
| b |
| e |
| a |
| b |
| e |
∴
| a |
| 1 |
| 7 |
| e |
| b |
| 10 |
| 7 |
| e |
| a |
| b |
对于B，存在相异实数λ，μ，使λ
| a |
| b |
| a |
| b |
对于C，x
| a |
| b |
| 0 |
| a |
| b |
对于D，已知梯形ABCD中，
| AB |
| a |
| CD |
| b |
故答案为：AB．
点评：本题考查命题的真假的判断，向量共线条件的应用与判断，基本知识的综合应用．
练习册系列答案
相关题目
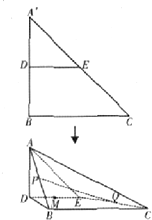如图，在Rt△A′BC中，A′B=BC=2，D，E分别是A′B，A′C的中点，将△A′DE沿线段DE折起到△ADE，使平面ADE⊥平面DBCE．