题目内容
在△ABC中，a：b：c=3：3：5，
的值 ．
| 2sinA-sinB |
| sinC |
考点：正弦定理
专题：解三角形
分析：先利用a，b，c的关系式设出分别设出a，b和c，利用正弦定理把题设转换成边，代入即可．
解答：
解：∵a：b：c=3：3：5，
∴设a=3t，b=3t，c=5t，
由正弦定理知
=
=
=
，
故答案为：
∴设a=3t，b=3t，c=5t，
由正弦定理知
| 2sinA-sinB |
| sinC |
| 2a-b |
| c |
| 6t-3t |
| 5t |
| 3 |
| 5 |
故答案为：
| 3 |
| 5 |
点评：本题主要考查了正弦定理的应用．正弦定理在解三角形问题中常用来对边角问题进行转换．
练习册系列答案
一课一练课时达标系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
若复数z满足iz=2+4i，则在复平面内，z的共轭复数
对应的点的坐标是（ ）
. |
| z |
| A、（2，4） |
| B、（2，-4） |
| C、（4，-2） |
| D、（4，2） |
小乐与小波在学了变量的相关性之后，两人约定回家去利用自己各自记录的6-10岁的身高记录作为实验数据，进行回归分析，探讨年龄x（岁）与身高y（cm）之间的线性相关性．经计算小乐与小波求得的线性回归直线分别为l1，l2，在认真比较后，两人发现他们这五年身高的平均值都为110cm，而且小乐的五组实验数据均满足所求的直线方程，小波则只有两组实验数据满足所求直线方程．下列说法错误的是（ ）
| A、直线l1，l2一定有公共点（8，110） |
| B、在两人的回归分析中，小乐求得的线性相关系数r=1，小波求得的线性相关系数r∈（0，1） |
| C、在小乐的回归分析中，他认为x与y之间完全线性相关，所以自己的身高y（cm）与年龄x（岁）成一次函数关系，利用l1可以准确预测自己20岁的身高 |
| D、在小波的回归分析中，他认为x与y之间不完全线性相关，所以自己的身高y（cm）与年龄x（岁）成相关关系，利用l2只可以估计预测自己20岁的身高 |
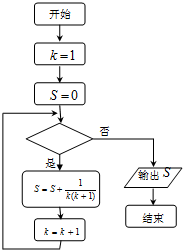
如果执行如图的程序框图，那么输出的S=
，那么判断框内是（ ）
| 2013 |
| 2014 |
| A、k≤2013？ |
| B、k≤2014？ |
| C、k≥2013？ |
| D、k≥2014？ |