题目内容
（1）已知a+b=2
，求证：a2+b2≥4．
（2）已知a＞b＞c，求证：
+
≥
．
| 2 |
（2）已知a＞b＞c，求证：
| 1 |
| a-b |
| 1 |
| b-c |
| 4 |
| a-c |
考点：基本不等式
专题：不等式的解法及应用
分析：（1）利用2（a2+b2）≥（a+b）2即可得出．
（2）由a＞b＞c，可得a-b＞0，b-c＞0，a-c＞0，可得
+
≥
?
+
≥4．
而
+
=
+
化简后利用基本不等式即可．
（2）由a＞b＞c，可得a-b＞0，b-c＞0，a-c＞0，可得
| 1 |
| a-b |
| 1 |
| b-c |
| 4 |
| a-c |
| a-c |
| a-b |
| a-c |
| b-c |
而
| a-c |
| a-b |
| a-c |
| b-c |
| (a-b)+(b-c) |
| a-b |
| (a-b)+(b-c) |
| b-c |
解答：
证明：（1）∵a+b=2
，
∴2（a2+b2）≥（a+b）2=(2
)2=8，
∴a2+b2≥4．
（2）∵a＞b＞c，∴a-b＞0，b-c＞0，a-c＞0，
∴
+
≥
?
+
≥4．
而
+
=
+
=2+
+
≥2+2
=4，当且仅当b-c=a-b时取等号．
因此原式成立．
| 2 |
∴2（a2+b2）≥（a+b）2=(2
| 2 |
∴a2+b2≥4．
（2）∵a＞b＞c，∴a-b＞0，b-c＞0，a-c＞0，
∴
| 1 |
| a-b |
| 1 |
| b-c |
| 4 |
| a-c |
| a-c |
| a-b |
| a-c |
| b-c |
而
| a-c |
| a-b |
| a-c |
| b-c |
| (a-b)+(b-c) |
| a-b |
| (a-b)+(b-c) |
| b-c |
=2+
| b-c |
| a-b |
| a-b |
| b-c |
|
因此原式成立．
点评：本题考查了变形利用基本不等式的性质，属于中档题．
练习册系列答案
相关题目
在△ABC中，D为BC边上一点，DC=2BD，AD=
，∠ADC=45°，若AC=
AB，则BD等于（ ）
| 2 |
| 2 |
A、2+
| ||
| B、4 | ||
C、2+
| ||
D、3+
|
一个棱锥被平行于底面的平面所截，若截面面积与底面面积之比为4：9，则此棱锥的侧棱被分成的上、下两部分长度之比为（ ）
| A、4：9 | ||
| B、2：1 | ||
| C、2：3 | ||
D、2：
|
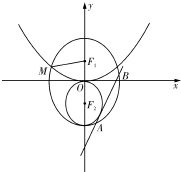已知F1，F2是椭圆C1：