题目内容
一个棱锥被平行于底面的平面所截,若截面面积与底面面积之比为4:9,则此棱锥的侧棱被分成的上、下两部分长度之比为( )
| A、4:9 | ||
| B、2:1 | ||
| C、2:3 | ||
D、2:
|
考点:旋转体(圆柱、圆锥、圆台)
专题:空间位置关系与距离
分析:由截面与底面为相似多边形,可得小棱锥侧棱与大棱锥侧棱之比为2:3,所以原棱锥的侧棱被分成的两部分之比为2:1.
解答:
解:由截面与底面为相似多边形,且截面面积与底面面积之比为4:9,
∴小棱锥侧棱与大棱锥侧棱之比为2:3,
∴原棱锥的侧棱被分成的两部分之比为2:1.
故选:B
∴小棱锥侧棱与大棱锥侧棱之比为2:3,
∴原棱锥的侧棱被分成的两部分之比为2:1.
故选:B
点评:本题考查的知识点是圆锥的几何特征,其中根据相似的性质,及截面面积与底面面积之比得到相似比是解答的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
△ABC中,若sinB•cosA<0,则三角形的形状为( )
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、等腰直角三角形 |
若不等式(m-1)x2+(m-1)x+2>0的解集是R,则m的范围是( )
| A、(1,9) |
| B、(-∞,1]∪(9,+∞) |
| C、[1,9) |
| D、(-∞,1)∪(9,+∞) |
已知a>0,b>0,且H=max{
,
},其中maxA表示数集A中的最大数.则下列结论中正确的是( )
| 1 |
| a |
| a2+b2 |
| b |
A、H有最大值
| ||||
B、H有最小值
| ||||
C、H有最小值
| ||||
D、H有最大值
|
已知i为虚数单位,a,b∈R,i(a+i)=b+2i,则a+b等于( )
| A、-1 | B、1 | C、-3 | D、3 |
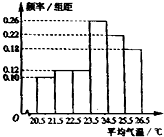 如图是根据部分城市某年6月份的平均气温(单位:℃)数据得到的样本频率分布直方图,其中平均气温的范围是[20.5,26.5],样本数据的分组为[20.5,21.5),[21.5,22.5),[22.5,23.5),[23.5,24.5),[24.5,25.5),[25.5,26.5].已知样本中平均气温低于22.5℃的城市个数为11,则样本中平均气温不低于25.5℃的城市个数为( )
如图是根据部分城市某年6月份的平均气温(单位:℃)数据得到的样本频率分布直方图,其中平均气温的范围是[20.5,26.5],样本数据的分组为[20.5,21.5),[21.5,22.5),[22.5,23.5),[23.5,24.5),[24.5,25.5),[25.5,26.5].已知样本中平均气温低于22.5℃的城市个数为11,则样本中平均气温不低于25.5℃的城市个数为( )