题目内容
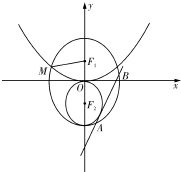 已知F1,F2是椭圆C1:
已知F1,F2是椭圆C1:| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
| 3 |
(1)求椭圆C1的方程;
(2)与圆x2+(y+1)2=1相切的直线l:y=k(x+t),kt≠0交椭圆C于A,B两点,若椭圆C上一点P满足
| OA |
| OB |
| OP |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由C2:x2=4y,知F1(0,1),c=1,设M(x0,y0),x0<0,由已知条件推导出x0=-
,y0=
,由此能求出椭圆C1的方程.
(2)由直线l:y=k(x+t),t≠0与圆x2+(y+1)2=1相切,求出k=
,且t2≠1,联立y=k(x+t)与
+
=1,得(4+3k2)x2+6k2tx+3k2t2-12=0,由此利用韦达定理结合已知条件能求出λ的取值范围.
2
| ||
| 3 |
| 2 |
| 3 |
(2)由直线l:y=k(x+t),t≠0与圆x2+(y+1)2=1相切,求出k=
| 2t |
| 1-t2 |
| y2 |
| 4 |
| x2 |
| 3 |
解答:
解:(1)由C2:x2=4y,知F1(0,1),c=1,设M(x0,y0),x0<0,
∵M在抛物线C2上,∴x0 2=4y0,①
又|MF1|=
,∴y0+1=
,②
由①②得x0=-
,y0=
,
∵点M在椭圆上,
∴2a=|MF1|+|MF2|=
+
=4,
∴a=2,b2=4-1=3,
∴椭圆C1的方程为
+
=1.
(2)由直线l:y=k(x+t),t≠0与圆x2+(y+1)2=1相切,
∴
=1,∵k≠0,∴k=
,且t2≠1,③
联立y=k(x+t)与
+
=1,
消去y得(4+3k2)x2+6k2tx+3k2t2-12=0,
设A(x1,y1),B(x2,y2),则x1+x2=-
,
y1+y2=k(x1+x2)+2kt=
,
∵λ
=
+
=(x1+x2,y1+y2),
∴P(
,
),
又点P在椭圆C1上,∴
+
=1,
∴λ2=
,④
由kt≠0,
把③代入④,得λ2=
,又t≠0,t2≠1,
∴(
)2+
+1>0,且(
)2+
+1≠3,
∴0<λ2<4,且λ2≠
,
∴λ的取值范围是(-2,-
)∪(-
,0)∪(0,
)∪(
,2).
∵M在抛物线C2上,∴x0 2=4y0,①
又|MF1|=
| 5 |
| 3 |
| 5 |
| 3 |
由①②得x0=-
2
| ||
| 3 |
| 2 |
| 3 |
∵点M在椭圆上,
∴2a=|MF1|+|MF2|=
| 5 |
| 3 |
(-
|
∴a=2,b2=4-1=3,
∴椭圆C1的方程为
| y2 |
| 4 |
| x2 |
| 3 |
(2)由直线l:y=k(x+t),t≠0与圆x2+(y+1)2=1相切,
∴
| |kt+1| | ||
|
| 2t |
| 1-t2 |
联立y=k(x+t)与
| y2 |
| 4 |
| x2 |
| 3 |
消去y得(4+3k2)x2+6k2tx+3k2t2-12=0,
设A(x1,y1),B(x2,y2),则x1+x2=-
| 6k2t |
| 4+3k2 |
y1+y2=k(x1+x2)+2kt=
| 8kt |
| 4+3k2 |
∵λ
| OP |
| OA |
| OB |
∴P(
| -6k2t |
| (4+3k2)λ |
| 8kt |
| (4+3k2)λ |
又点P在椭圆C1上,∴
| 12k4t2 |
| (4+3k2)2λ2 |
| 16k2t2 |
| (4+3k2)2λ2 |
∴λ2=
| 4k2t2 |
| 4+3k2 |
由kt≠0,
把③代入④,得λ2=
| 4 | ||||
(
|
∴(
| 1 |
| t2 |
| 1 |
| t2 |
| 1 |
| t2 |
| 1 |
| t2 |
∴0<λ2<4,且λ2≠
| 4 |
| 3 |
∴λ的取值范围是(-2,-
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
点评:本题考查椭圆方程的求法,考查实数的取值范围的求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
若曲线f(x)=ax2-lnx在点M(1,a)处的切线平行于x轴,则a的值为( )
| A、-2 | ||
| B、2 | ||
C、-
| ||
D、
|
已知i为虚数单位,a,b∈R,i(a+i)=b+2i,则a+b等于( )
| A、-1 | B、1 | C、-3 | D、3 |
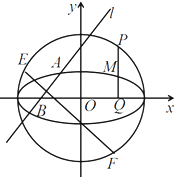 如图,P是⊙O:x2+y2=4上任意一点,PQ⊥x轴,Q为垂足.设PQ的中点为M.
如图,P是⊙O:x2+y2=4上任意一点,PQ⊥x轴,Q为垂足.设PQ的中点为M. 研究“刹车距离”对于安全行车及分析交通事故责任都有一定的作用,所谓“刹车距离”就是指行驶中的汽车,从刹车开始到停止,由于惯性的作用而又继续向前滑行的一段距离.为了测定某种型号汽车的刹车性能(车速不超过140km/h),对这种汽车进行测试,测得的数据如表:
研究“刹车距离”对于安全行车及分析交通事故责任都有一定的作用,所谓“刹车距离”就是指行驶中的汽车,从刹车开始到停止,由于惯性的作用而又继续向前滑行的一段距离.为了测定某种型号汽车的刹车性能(车速不超过140km/h),对这种汽车进行测试,测得的数据如表: