题目内容
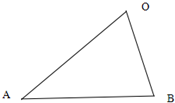在△OAB中，| OA |
| a |
| OB |
| b |
| a |
| b |
| a |
| b |
（1）求|
| a |
| b |
（2）若（
| ||
|
|
| ||
|
|
| a |
| b |
| AB |
| AM |
| BA |
| BN |
| OM |
| ON |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：（1）运用向量数量积的性质：向量的平方即为模的平方，计算即可得到；
（2）通过条件（
+
）•（
-
）=0，化简整理可得|
|=|
|，由（1）的结论即有△OAB为正三角形，再由向量垂直的条件，即可计算得到所求值．
（2）通过条件（
| ||
|
|
| ||
|
|
| a |
| b |
| a |
| b |
解答：
解：（1）由于|
-
|=2，则|
-
|2=（
-
）2=
2+
2-2
•
=4，
又
•
=2，
则有|
|2+|
|2=
2+
2=8；
（2）由（
+
）•（
-
）=0，
则
+
-
-
=|
|-|
|+
-
=（|
|-|
|）（1+
）=0，
则有|
|=|
|，由（1）的结论得|
|=|
|=2，
又|
|=|
-
|=2，所以△OAB为正三角形，
则
•
=（
+
）•
，
因为N为AB的中点，ON⊥AB，
从而
•
=0，|
|=
×2=
，
则有
•
=（
）2=3．
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
又
| a |
| b |
则有|
| a |
| b |
| a |
| b |
（2）由（
| ||
|
|
| ||
|
|
| a |
| b |
则
| ||
|
|
| ||||
|
|
| ||||
|
|
| ||
|
|
| a |
| b |
| 2 | ||
|
|
| 2 | ||
|
|
| a |
| b |
| 2 | ||||
|
|
则有|
| a |
| b |
| a |
| b |
又|
| AB |
| a |
| b |
则
| OM |
| ON |
| ON |
| NM |
| ON |
因为N为AB的中点，ON⊥AB，
从而
| ON |
| NM |
| ON |
| ||
| 2 |
| 3 |
则有
| OM |
| ON |
| ON |
点评：本题考查向量的数量积的性质，考查正三角形的性质，考查运算能力，运用向量垂直的条件是解题的关键．
练习册系列答案
黎明文化寒假作业系列答案
寒假天地重庆出版社系列答案
相关题目
已知复数z1=3+4i，z2=t+i，且z1•z2是实数，则实数t等于（ ）
A、
| ||
B、
| ||
C、-
| ||
D、-
|
如图，已知三棱锥P-ABC中，PA⊥平面 ABC，△ABC是正三角形，AC=2 PA=2，D、E分别为棱 AC和 BC的中点．