题目内容
已知向量
=(1,
),
=(-1,0),则|
+2
|= .
| a |
| 3 |
| b |
| a |
| b |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:利用向量的坐标运算、模的计算公式即可得出.
解答:
解:∵向量
=(1,
),
=(-1,0),
∴
+2
=(1,
)+2(-1,0)=(-1,
),
∴|
+2
|=
=2.
故答案为:2.
| a |
| 3 |
| b |
∴
| a |
| b |
| 3 |
| 3 |
∴|
| a |
| b |
12+(
|
故答案为:2.
点评:本题考查了数量积运算性质、模的计算公式、向量坐标运算,考查了计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知i为虚数单位,则复数z=(-1-2i)i在复平面内对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
某几何体的三视图如图所示,则该几何体的体积是( )


| A、2 | B、≥ | C、∞ | D、3 |
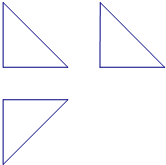 如图,某三棱锥的三视图都是直角边为
如图,某三棱锥的三视图都是直角边为| 2 |
A、
| ||
| B、6π | ||
C、2
| ||
| D、8π |
函数f(x)=log2(x-1)的零点是( )
| A、(1,0) | B、(2,0) |
| C、1 | D、2 |
椭圆2x2+y2=1上的点到直线y=
x-4的距离的最小值是( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 四边形ABCD是单位圆O的内接正方形,它可以绕原点O转动,已知点P的坐标是(3,4),M、N分别是边AB、BC的中点,则
四边形ABCD是单位圆O的内接正方形,它可以绕原点O转动,已知点P的坐标是(3,4),M、N分别是边AB、BC的中点,则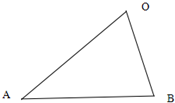 在△OAB中,
在△OAB中,