题目内容
函数f(x)=log
x+1 在x∈[
,8)上的值域为 .
| 1 |
| 2 |
| 1 |
| 4 |
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:首先判断对数函数的单调性,进一步利用函数的定义域求函数的值域.
解答:
解:令函数g(x)=log
x,由于对数函数的底数为
,则函数为减函数.
由于x∈[
,8)时,所以函数的值域为g(x)∈(-3,2]
所以:函数f(x)=log
x+1的值域为:f(x)∈(-2,3]
故答案为:(-2,3]
| 1 |
| 2 |
| 1 |
| 2 |
由于x∈[
| 1 |
| 4 |
所以:函数f(x)=log
| 1 |
| 2 |
故答案为:(-2,3]
点评:本题考查的知识要点:对数函数的单调性的应用,利用函数的定义域求函数的值域.属于基础题型.

练习册系列答案
相关题目
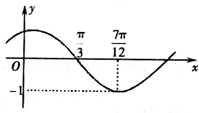 函数f(x)=Asin(ωx+φ)(其中A>0,ω,0,|φ|<
函数f(x)=Asin(ωx+φ)(其中A>0,ω,0,|φ|<| π |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向右平移
| ||
D、向左平移
|
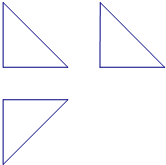 如图,某三棱锥的三视图都是直角边为
如图,某三棱锥的三视图都是直角边为| 2 |
A、
| ||
| B、6π | ||
C、2
| ||
| D、8π |
 四边形ABCD是单位圆O的内接正方形,它可以绕原点O转动,已知点P的坐标是(3,4),M、N分别是边AB、BC的中点,则
四边形ABCD是单位圆O的内接正方形,它可以绕原点O转动,已知点P的坐标是(3,4),M、N分别是边AB、BC的中点,则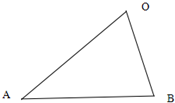 在△OAB中,
在△OAB中,