题目内容
已知函数f(x)=
,且函数y=f(x)+x恰有3个不同的零点,则实数a的取值范围是 .
|
考点:函数零点的判定定理
专题:函数的性质及应用
分析:根据题意,原函数的零点可转化为y=f(x)与y=-x的图象交点的个数问题,然后据题意画出它们的图象,判断何时有三个交点即可.
解答:
解:因为当x≥0的时候,f(x)=f(x-1),
当x∈[0,1)时,x-1∈[-1,0),此时f(x)=f(x-1)=a+(x-1)2+2(x-1)
当x∈[1,2)时,x-2∈[-1,0),此时f(x)=f(x-2)=f(x-2)=a+(x-2)2+2(x-2)
依此类推,f(x)在x<0时为二次函数y=a+x2+2x=(x+1)2+a-1,
在x≥0上为周期为1的函数,重复部分为y=a+x2+2x=(x+1)2+a-1在区间[-1,0)上的部分.
二次函数y=a+x2+2x=(x+1)2+a-1顶点为(-1,a-1),
y=f(x)+x恰有3个不同的零点,即y=f(x)与y=-x的图象有三个不同的交点.
做出它们的图象如下:
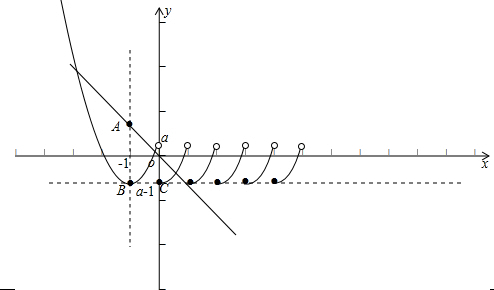
可知:只要是函数y=f(x)图象上的点C在直线y=-x上或在该直线的下方,就能保证直线和函数y=f(x)的图象产生三个不同的交点.
因此只需a-1≤0,即a≤1即可.
故答案为(-∞,1].
当x∈[0,1)时,x-1∈[-1,0),此时f(x)=f(x-1)=a+(x-1)2+2(x-1)
当x∈[1,2)时,x-2∈[-1,0),此时f(x)=f(x-2)=f(x-2)=a+(x-2)2+2(x-2)
依此类推,f(x)在x<0时为二次函数y=a+x2+2x=(x+1)2+a-1,
在x≥0上为周期为1的函数,重复部分为y=a+x2+2x=(x+1)2+a-1在区间[-1,0)上的部分.
二次函数y=a+x2+2x=(x+1)2+a-1顶点为(-1,a-1),
y=f(x)+x恰有3个不同的零点,即y=f(x)与y=-x的图象有三个不同的交点.
做出它们的图象如下:

可知:只要是函数y=f(x)图象上的点C在直线y=-x上或在该直线的下方,就能保证直线和函数y=f(x)的图象产生三个不同的交点.
因此只需a-1≤0,即a≤1即可.
故答案为(-∞,1].
点评:本题考查了利用函数的图象判断函数零点的个数问题的解题思路,要注意准确画图.

练习册系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积是( )


| A、2 | B、≥ | C、∞ | D、3 |
椭圆2x2+y2=1上的点到直线y=
x-4的距离的最小值是( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 在△OAB中,
在△OAB中,