题目内容
已知复数z1=3+4i，z2=t+i，且z1•z2是实数，则实数t等于（ ）
A、
| ||
B、
| ||
C、-
| ||
D、-
|
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：由复数代数形式的乘除运算化简，然后由虚部等于0求得t的值．
解答：
解：∵z1=3+4i，z2=t+i，
∴z1•z2=（3+4i）（t+i）=（3t-4）+（4t+3）i，
由z1•z2是实数，得4t+3=0，即t=-
．
故选：D．
∴z1•z2=（3+4i）（t+i）=（3t-4）+（4t+3）i，
由z1•z2是实数，得4t+3=0，即t=-
| 3 |
| 4 |
故选：D．
点评：本题考查了复数代数形式的乘除运算，考查了复数的基本概念，是基础题．
练习册系列答案
相关题目
已知不等式组
所表示的平面区域为D，若直线y=kx-3与平面区域D有公共点，则k的取值范围是（ ）
|
| A、[-3，3] | ||||
B、（-∞，
| ||||
| C、（-∞，-3]∪[3，+∞） | ||||
D、[-
|
已知i为虚数单位，则复数z=（-1-2i）i在复平面内对应的点位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知i为虚数单位，则复数z=
在复平面内对应的点位于（ ）
| 1+2i |
| i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
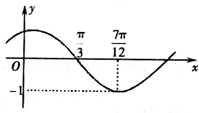函数f（x）=Asin（ωx+φ）（其中A＞0，ω，0，|φ|＜| π |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向右平移
| ||
D、向左平移
|
某几何体的三视图如图所示，则该几何体的体积是（ ）
| A、2 | B、≥ | C、∞ | D、3 |
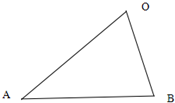在△OAB中，