题目内容
2.现有2门不同的考试要安排在连续的5天之内进行,每天最多考一门,且不能连续两天有考试,则不同的安排方案有( )| A. | 6种 | B. | 8种 | C. | 12种 | D. | 16种 |
分析 若第一门安排在开头或结尾,则第二门有3种安排方法.若第一门安排在中间的3天中,则第二门有2种安排方法,根据分步计数原理分别求出安排方案种数,相加即得所求.
解答 解:若第一门安排在开头或结尾,则第二门有3种安排方法,这时,共有${C}_{2}^{1}×$3=6种方法.
若第一门安排在中间的3天中,则第二门有2种安排方法,这时,共有3×2=6种方法.
综上可得,所有的不同的考试安排方案种数有6+6=12种,
故选C.
点评 本题考查排列、组合及简单计数问题,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
12.已知函数f(x)=e2x-aex+2x在R上是增函数,则实数a的取值范围是( )
| A. | (2,4] | B. | (-∞,4] | C. | (3,4) | D. | [3,4) |
13.命题“若a>b,则a+c>b+c”的否命题是( )
| A. | 若a≤b,则a+c≤b+c | B. | 若a+c≤b+c,则a≤b | C. | 若a+c>b+c,则a>b | D. | 若a>b,则a+c≤b+c |
14.如图是一个三棱柱的正视图和俯视图,其俯视图是面积为8$\sqrt{2}$的矩形,则该三棱柱的体积是( )
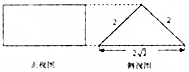

| A. | 8 | B. | 4$\sqrt{2}$ | C. | 16 | D. | $\frac{16}{3}$ |
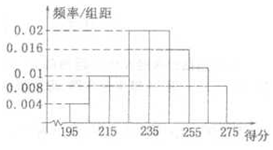 某高校组织自主招生考试,共有2 000名学生报名参加了笔试,成绩均介于195分到275分 之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分成八组:第一组[195,205),第二组[205,215),…,第八组[265,275].如图是按上述分组方法得到的频率分布直方图,已知笔试成绩在260分以上(含260分)的同学取得面试资格.
某高校组织自主招生考试,共有2 000名学生报名参加了笔试,成绩均介于195分到275分 之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分成八组:第一组[195,205),第二组[205,215),…,第八组[265,275].如图是按上述分组方法得到的频率分布直方图,已知笔试成绩在260分以上(含260分)的同学取得面试资格.