题目内容
7.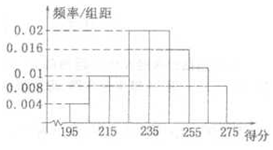 某高校组织自主招生考试,共有2 000名学生报名参加了笔试,成绩均介于195分到275分 之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分成八组:第一组[195,205),第二组[205,215),…,第八组[265,275].如图是按上述分组方法得到的频率分布直方图,已知笔试成绩在260分以上(含260分)的同学取得面试资格.
某高校组织自主招生考试,共有2 000名学生报名参加了笔试,成绩均介于195分到275分 之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分成八组:第一组[195,205),第二组[205,215),…,第八组[265,275].如图是按上述分组方法得到的频率分布直方图,已知笔试成绩在260分以上(含260分)的同学取得面试资格.(Ⅰ)估计所有参加笔试的2000名学生中,取得面试资格的学生人数;
(Ⅱ)面试时,每位考生抽取三个问题(每人在 回答三个问题时对每一个问题正确回答的概率均为$\frac{1}{2}$).若三个问题全答错,则不能取得该校的自主招生资格;若三个问题均回答正确且笔试成绩在270分以上,则 获A类资格(不参加高考,直接录取);其它情况下获B类资格(参加高考,降分录取),武估计获得A类资格和B类资格的人数.
分析 (Ⅰ)根据频率和为1,求出对应的频率以及成绩在260分以上的频率,计算对应的频数;
(Ⅱ)计算成绩在270分以上的人数,求出其中三题都答对的人数X的可能取值,
以及三题都答错的人数Y,计算对应的数学期望值.
解答 解:(Ⅰ)设第i(i=1,2,3,…,8)组的频率为fi,
由频率分布图知,
f7=1-(0.004+0.01+0.01+0.02+0.02+0.0016+0.008)×10=0.12;
所以成绩在260分以上的同学的概率为
P≈$\frac{{f}_{7}}{2}$+f8=0.14,
故这2000名同学中,取得面试资格的约为280人; …(4分)
(Ⅱ)成绩在270分以上的同学的人数约为
$\frac{{f}_{8}}{2}$×2000=80(人),
设80人中三题都答对的人数为X,则
X~B($\frac{1}{8}$,80),E(X)=$\frac{1}{8}$×80=10,
所以,获得A类资格的人数约为10人;
设280人中三题都答错的人数为Y,则
Y~B($\frac{1}{8}$,280),E(Y)=$\frac{1}{8}$×280=35,
所以,获得B类资格的人数约为
280-10-35=235(人). …(12分)
点评 本题考查了频率分布直方图以及n次独立重复事件的数学期望值的计算问题,是综合题.

练习册系列答案
相关题目
18.已知i为虚数单位,则复数$\frac{2016}{1+i}$的虚部是( )
| A. | -1008 | B. | -1008i | C. | 1008 | D. | 2016 |
2.现有2门不同的考试要安排在连续的5天之内进行,每天最多考一门,且不能连续两天有考试,则不同的安排方案有( )
| A. | 6种 | B. | 8种 | C. | 12种 | D. | 16种 |
16.复数z满足(z-i)(2-i)=5,则z所对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |