题目内容
11.在平面直角坐标系xOy中,直线l的参数方程为$\left\{\begin{array}{l}{x=-2+t}\\{y=-2t}\end{array}\right.$(t为参数),圆C的普通方程为x2+y2-2y=0,以O为极点,x轴的正半轴为极轴,建立极坐标系.(1)求直线l的极坐标方程;
(2)设M(ρ,θ)(ρ≥0,0≤θ<2π)为直线l上一动点,MA切圆C于点A,求|MA|的最小值,及此时点M的极坐标.
分析 (1)直线l的参数方程消去参数t,得直线l的普通方程,由此能求出直线l的极坐标方程.
(2)圆C的普通方程为x2+y2-2y=0,圆心C(0,1),半径r=1,求出圆心C(0,1)到直线l的距离d=$\sqrt{5}$,从而|MA|的最小值|MA|min=$\sqrt{{d}^{2}-{r}^{2}}$=2,此时${k}_{OM}=\frac{1}{2}$,直线OM的方程为:y=$\frac{1}{2}x+1$,联立$\left\{\begin{array}{l}{y=\frac{1}{2}x+1}\\{2x+y+4=0}\end{array}\right.$,求出M(-2,0),由此有求出点M的极坐标.
解答 解:(1)∵直线l的参数方程为$\left\{\begin{array}{l}{x=-2+t}\\{y=-2t}\end{array}\right.$(t为参数),
∴消去参数t,得直线l的普通方程为:2x+y+4=0,
∴直线l的极坐标方程为2ρcosθ+ρsinθ+4=0.
(2)圆C的普通方程为x2+y2-2y=0,圆心C(0,1),半径r=1,
M(ρ,θ)(ρ≥0,0≤θ<2π)为直线l上一动点,MA切圆C于点A,
∵圆心C(0,1)到直线l的距离d=$\frac{|0+1+4|}{\sqrt{4+1}}$=$\sqrt{5}$,
∴|MA|的最小值|MA|min=$\sqrt{{d}^{2}-{r}^{2}}$=$\sqrt{5-1}$=2,
此时${k}_{OM}=\frac{1}{2}$,直线OM的方程为:y=$\frac{1}{2}x+1$,
联立$\left\{\begin{array}{l}{y=\frac{1}{2}x+1}\\{2x+y+4=0}\end{array}\right.$,得x=-2,y=0,∴M(-2,0),
∴$ρ=\sqrt{4+0}$=2,θ=π,
∴点M的极坐标为M(2,π).
点评 本题考查直线、曲线的极坐标方程的求法,考查点的极坐标的求法,是中档题,解题时要认真审题,注意参数方程、直角坐标方程、极坐标方程互化公式的合理运用.

 阅读快车系列答案
阅读快车系列答案| A. | 6种 | B. | 8种 | C. | 12种 | D. | 16种 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | $\frac{4}{3}$ |
| A. | [-2,0] | B. | [-2,2] | C. | [0,2] | D. | [0,4] |
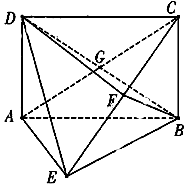 如图,四边形ABCD是矩形,DA⊥平面ABE,AE=EB=BC=2,F为线段CE上一点,且BF⊥平面ACE,AC交BD于点G.
如图,四边形ABCD是矩形,DA⊥平面ABE,AE=EB=BC=2,F为线段CE上一点,且BF⊥平面ACE,AC交BD于点G.