题目内容
14.如图是一个三棱柱的正视图和俯视图,其俯视图是面积为8$\sqrt{2}$的矩形,则该三棱柱的体积是( )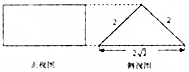
| A. | 8 | B. | 4$\sqrt{2}$ | C. | 16 | D. | $\frac{16}{3}$ |
分析 由题意该三棱柱ABC-A1B1C1中,四边形ABCD是长AA1=4,宽AB=2$\sqrt{2}$的矩形,△ABC是直角边AC=BC=2的等腰直角三角形,由此能求出该三棱柱的体积.
解答 解: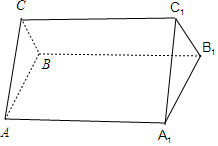 由三棱柱的正视图和俯视图及其俯视图是面积为8$\sqrt{2}$的矩形,
由三棱柱的正视图和俯视图及其俯视图是面积为8$\sqrt{2}$的矩形,
知该三棱柱是如图所示的三棱柱ABC-A1B1C1,
且四边形ABCD是长AA1=4,宽AB=2$\sqrt{2}$的矩形,
△ABC是直角边AC=BC=2的等腰直角三角形,
∴该三棱柱的体积V=S△ABC×AA1=$\frac{1}{2}×2×2×4$=8.
故选:A.
点评 本题考查柱、锥、台体的体积,考查推理论证能力,考查空间想象能力与计算能力,考查等价转化思想及数形结合思想,是中档题.

练习册系列答案
相关题目
2.现有2门不同的考试要安排在连续的5天之内进行,每天最多考一门,且不能连续两天有考试,则不同的安排方案有( )
| A. | 6种 | B. | 8种 | C. | 12种 | D. | 16种 |
3.在三棱锥ABCD中,BC⊥CD,Rt△BCD斜边上的高为1,三棱锥ABCD的外接球的直径是AB,若该外接球的表面积为16π,则三棱锥ABCD体积的最大值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | $\frac{4}{3}$ |
4.已知等比数列{an}的首项为1,若4a1,2a2,a3成等差数列,则数列{$\frac{1}{{a}_{n}}$}的前5项和为( )
| A. | $\frac{33}{16}$ | B. | 2 | C. | $\frac{31}{16}$ | D. | $\frac{31}{64}$ |