题目内容
13.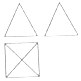 某四棱锥的三视图如图所示,正视图、侧视图都是边长为$2\sqrt{3}$的等边三角形,俯视图是一个正方形,则此四棱锥的体积是( )
某四棱锥的三视图如图所示,正视图、侧视图都是边长为$2\sqrt{3}$的等边三角形,俯视图是一个正方形,则此四棱锥的体积是( )| A. | $8\sqrt{3}$ | B. | 12 | C. | 24 | D. | 36 |
分析 由三视图知此四棱锥为正四棱锥,底面是边长为$2\sqrt{3}$的正方形,正四棱锥的高即等边三角形的高为3.
解答 解:由三视图知此四棱锥为正四棱锥,底面是边长为$2\sqrt{3}$的正方形,正四棱锥的高即等边三角形的高为3,体积是$V=\frac{1}{3}×2\sqrt{3}×2\sqrt{3}×3=12$.
故选:B.
点评 本题考查了正四棱锥的三视图及其体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
19.已知A,B,C三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如表(单位:小时).
(1)试估计C班学生人数;
(2)从A班和B班抽出来的学生中各选一名,记A班选出的学生为甲,B班选出的学生为乙,求甲的锻炼时间大于乙的锻炼时间的概率.
| A 班 | 6 | 6.5 | 7 | |
| B 班 | 6 | 7 | 8 | |
| C 班 | 5 | 6 | 7 | 8 |
(2)从A班和B班抽出来的学生中各选一名,记A班选出的学生为甲,B班选出的学生为乙,求甲的锻炼时间大于乙的锻炼时间的概率.
1.A、F分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左顶点和右焦点,A、F在双曲线的一条渐近线上的射影分别为B、Q,O为坐标原点,△ABO与△FQO的面积之比为$\frac{1}{2}$,则该双曲线的离心率为( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{2}$ |
2.设A,B是两个非空集合,定义集合A-B={x|x∈A且x∉B}.若A={x∈N|0≤x≤5},B={x|x2-7x+10<0},则A-B=( )
| A. | {0,1} | B. | {1,2} | C. | {0,1,2} | D. | {0,1,2,5} |
3.下列命题推断错误的是( )
| A. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 | |
| B. | 若p且q为假命题,则p,q均为假命题 | |
| C. | “x=-1”是“x2-5x-6=0”的充分不必要条件 | |
| D. | 命题p:存在x0∈R,使得x02+x0+1<0,则非p:任意x∈R,都有x2+x+1≥0 |
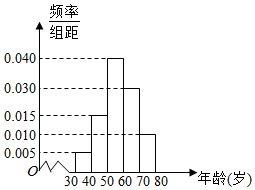 某研究小组到社区了解参加健美操运动人员的情况,用分层抽样的方法抽取了40人进行调查,按照年龄分成五个小组:[30,40],(40,50],(50,60],(60,70],(70,80],并绘制成如图所示的频率分布直方图.
某研究小组到社区了解参加健美操运动人员的情况,用分层抽样的方法抽取了40人进行调查,按照年龄分成五个小组:[30,40],(40,50],(50,60],(60,70],(70,80],并绘制成如图所示的频率分布直方图.