题目内容
2．设A，B是两个非空集合，定义集合A-B={x|x∈A且x∉B}．若A={x∈N|0≤x≤5}，B={x|x2-7x+10＜0}，则A-B=（ ）| A． | {0，1} | B． | {1，2} | C． | {0，1，2} | D． | {0，1，2，5} |
分析 化简集合A，B，利用A-B是集合A中的元素且不是B中的元素，求出A-B．
解答 解：∵A={x∈N|0≤x≤5}={0，1，2，3，4，5}，B={x|x2-7x+10＜0}=（2，5），
A-B={x|x∈A且x∉B}，
∴A-B={0，1，2，5}，
故选D．
点评 本题考查利用题中的定义求集合、考查二次不等式，比较基础．
练习册系列答案
相关题目
13．
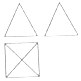某四棱锥的三视图如图所示，正视图、侧视图都是边长为$2\sqrt{3}$的等边三角形，俯视图是一个正方形，则此四棱锥的体积是（ ）
某四棱锥的三视图如图所示，正视图、侧视图都是边长为$2\sqrt{3}$的等边三角形，俯视图是一个正方形，则此四棱锥的体积是（ ）| A． | $8\sqrt{3}$ | B． | 12 | C． | 24 | D． | 36 |
10．设公比为q（q＞0）的等比数列{an}的前项和为Sn，若S2=3a2+2，S4=3a4+2，则a1=（ ）
| A． | -2 | B． | -1 | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
7．若${（{\frac{3}{{\sqrt{x}}}-\root{3}{x}}）^n}$的展开式中所有项系数的绝对值之和为1024，则该展开式中的常数项是（ ）
| A． | -270 | B． | 270 | C． | -90 | D． | 90 |
12．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的一个焦点与抛物线${y^2}=4\sqrt{3}x$的焦点重合，长轴长等于圆x2+y2-2x-15=0的半径，则椭圆C的方程为（ ）
| A． | $\frac{x^2}{4}+\frac{y^2}{3}=1$ | B． | $\frac{x^2}{16}+\frac{y^2}{12}=1$ | C． | $\frac{x^2}{4}+{y^2}=1$ | D． | $\frac{x^2}{16}+\frac{y^2}{4}=1$ |