题目内容
4.在一个长方体的三条棱长分别为3、8、9,若在该长方体上面钻一个圆柱形的孔后其表面积没有变化,则圆孔的半径为3.分析 设半径为r,由题意得减少的2个圆的面积=圆柱的侧面积,由此列出方程能求出圆孔的半径.
解答 解:设半径为r,
∵在一个长方体的三条棱长分别为3、8、9,在该长方体上面钻一个圆柱形的孔后其表面积没有变化,
∴减少的2个圆的面积=圆柱的侧面积,
∴2πr2=2πr×3,
解得r=3.
∴圆孔的半径为3.
故答案为:3.
点评 本题考查圆孔的半径的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
19.函数f(x)=sin2(x+$\frac{π}{4}$)-sin2(x-$\frac{π}{4}$)是( )
| A. | 最小正周期为2π的偶函数 | B. | 最小正周期为2π的奇函数 | ||
| C. | 最小正周期为π的偶函数 | D. | 最小正周期为π的奇函数 |
13.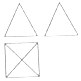 某四棱锥的三视图如图所示,正视图、侧视图都是边长为$2\sqrt{3}$的等边三角形,俯视图是一个正方形,则此四棱锥的体积是( )
某四棱锥的三视图如图所示,正视图、侧视图都是边长为$2\sqrt{3}$的等边三角形,俯视图是一个正方形,则此四棱锥的体积是( )
 某四棱锥的三视图如图所示,正视图、侧视图都是边长为$2\sqrt{3}$的等边三角形,俯视图是一个正方形,则此四棱锥的体积是( )
某四棱锥的三视图如图所示,正视图、侧视图都是边长为$2\sqrt{3}$的等边三角形,俯视图是一个正方形,则此四棱锥的体积是( )| A. | $8\sqrt{3}$ | B. | 12 | C. | 24 | D. | 36 |
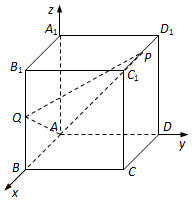 如图,在棱长为2的正方体ABCD-A1B1C1D1中,P为棱C1D1的中点,Q为棱BB1上的点,且BQ=λBB1(λ≠0).
如图,在棱长为2的正方体ABCD-A1B1C1D1中,P为棱C1D1的中点,Q为棱BB1上的点,且BQ=λBB1(λ≠0).