题目内容
5.近年来我国电子商务行业迎来蓬勃发展新机遇,2016年双11期间,某网络购物平台推销了A,B,C三种商品,某网购者决定抢购这三种商品,假设该名网购者都参与了A,B,C三种商品的抢购,抢购成功与否相互独立,且不重复抢购同一种商品,对A,B,C三件商品抢购成功的概率分别为a,b,$\frac{1}{4}({a>b})$,已知三件商品都被抢购成功的概率为$\frac{1}{24}$,至少有一件商品被抢购成功的概率为$\frac{3}{4}$.(1)求a,b的值;
(2)若购物平台准备对抢购成功的A,B,C三件商品进行优惠减免,A商品抢购成功减免2百元,B商品抢购成功减免4比百元,C商品抢购成功减免6百元.求该名网购者获得减免总金额(单位:百元)的分别列和数学期望.
分析 (Ⅰ)由题意利用相互独立及其对立事件的概率计算公式可得$\left\{{\begin{array}{l}{\frac{1}{4}ab=\frac{1}{24}}\\{1-(1-a)(1-\frac{1}{4})(1-b)=\frac{3}{4}}\end{array}}\right.$.
(Ⅱ)由题意,令网购者获得减免的总金额为随机变量X(单位:百元),则X的值可以为0,2,4,6,8,10,12.再利用相互独立事件的概率计算公式即可得出.
解答 解:(Ⅰ)由题意,得$\left\{{\begin{array}{l}{\frac{1}{4}ab=\frac{1}{24}}\\{1-(1-a)(1-\frac{1}{4})(1-b)=\frac{3}{4}}\end{array}}\right.$,
因为a>b,解得$\left\{{\begin{array}{l}{a=\frac{1}{2}}\\{b=\frac{1}{3}}\end{array}}\right.$. …(4分)
(Ⅱ)由题意,令网购者获得减免的总金额为随机变量X(单位:百元),
则X的值可以为0,2,4,6,8,10,12. …(5分)
而$P(X=0)=\frac{1}{2}×\frac{2}{3}×\frac{3}{4}=\frac{1}{4}$;$P(X=2)=\frac{1}{2}×\frac{2}{3}×\frac{3}{4}=\frac{1}{4}$;$P(X=4)=\frac{1}{2}×\frac{1}{3}×\frac{3}{4}=\frac{1}{8}$;$P(X=6)=\frac{1}{2}×\frac{2}{3}×\frac{1}{4}+\frac{1}{2}×\frac{1}{3}×\frac{3}{4}=\frac{5}{24}$;$P(X=8)=\frac{1}{2}×\frac{2}{3}×\frac{1}{4}=\frac{1}{12}$;$P(X=10)=\frac{1}{2}×\frac{1}{3}×\frac{1}{4}=\frac{1}{24}$;$P(X=12)=\frac{1}{2}×\frac{1}{3}×\frac{1}{4}=\frac{1}{24}$. …(9分)
所以X的分布列为:
| X | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
| P | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{8}$ | $\frac{5}{24}$ | $\frac{1}{12}$ | $\frac{1}{24}$ | $\frac{1}{24}$ |
点评 本题考查了相互独立及其对立事件的概率计算公式、分布列及其数学期望计算公式,考查了推理能力与计算能力,属于中档题.

 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案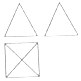 某四棱锥的三视图如图所示,正视图、侧视图都是边长为$2\sqrt{3}$的等边三角形,俯视图是一个正方形,则此四棱锥的体积是( )
某四棱锥的三视图如图所示,正视图、侧视图都是边长为$2\sqrt{3}$的等边三角形,俯视图是一个正方形,则此四棱锥的体积是( )| A. | $8\sqrt{3}$ | B. | 12 | C. | 24 | D. | 36 |
| A. | -2 | B. | -1 | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
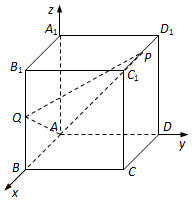 如图,在棱长为2的正方体ABCD-A1B1C1D1中,P为棱C1D1的中点,Q为棱BB1上的点,且BQ=λBB1(λ≠0).
如图,在棱长为2的正方体ABCD-A1B1C1D1中,P为棱C1D1的中点,Q为棱BB1上的点,且BQ=λBB1(λ≠0).