题目内容
18.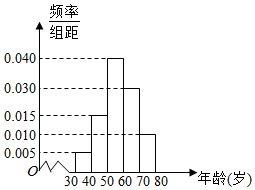 某研究小组到社区了解参加健美操运动人员的情况,用分层抽样的方法抽取了40人进行调查,按照年龄分成五个小组:[30,40],(40,50],(50,60],(60,70],(70,80],并绘制成如图所示的频率分布直方图.
某研究小组到社区了解参加健美操运动人员的情况,用分层抽样的方法抽取了40人进行调查,按照年龄分成五个小组:[30,40],(40,50],(50,60],(60,70],(70,80],并绘制成如图所示的频率分布直方图.(1)求该社区参加健美操运动人员的平均年龄;
(2)如果研究小组从该样本中年龄在[30,40]和(70,80]的6人中随机地抽取出2人进行深入采访,求被采访的2人,年龄恰好都在(70,80]内的概率.
分析 (1)利用组中值,即可求该社区参加健美操运动人员的平均年龄;
(2)利用列举法,确定基本事件的个数,即可求被采访的2人,年龄恰好都在(70,80]内的概率.
解答 解:(1)$\overline x=35×0.05+45×0.15+55×0.40+65×0.30+75×0.10=57.5$,
该社区参加健美操运动人员的平均年龄为57.5岁;…(5分)
(2)年龄在[30,40)的人员2人,依次记为a1、a2,年龄在[70,80]的人员4人,
依次记为b1、b2、b3、b4,从这6人中随机地选出2人有15种等可能的结果:a1a2、a1b1、a1b2、a1b3、a1b4、a2b1、a2b2、a2b3、a2b4、b1b2、b1b3、b1b4、b2b3、b2b4、b3b4;
记事件A:被采访的2人年龄恰好都在[70,80],则A包含6种结果,$P(A)=\frac{6}{15}=0.4$.
所以,被采访的2人年龄恰好都在[70,80]的概率为0.4.…(12分)
点评 本题考查频率分布直方图,考查概率的计算,确定基本事件的个数是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.命题?x>0,ln(x+1)>0的否定为( )
| A. | ?x0<0,ln(x0+1)<0 | B. | ?x0≤0,ln(x0+1)≤0 | C. | ?x0>0,ln(x0+1)<0 | D. | ?x0>0,ln(x0+1)≤0 |
6.某研究型学习小组调查研究”中学生使用智能手机对学习的影响”.部分统计数据如表:
参考数据:
参考公式:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d
(Ⅰ)试根据以上数据,运用独立性检验思想,指出有多大把握认为中学生使用智能手机对学习有影响?
(Ⅱ)研究小组将该样本中使用智能手机且成绩优秀的4位同学记为A组,不使用智能手机且成绩优秀的8位同学记为B组,计划从A组推选的2人和B组推选的3人中,随机挑选两人在学校升旗仪式上作“国旗下讲话”分享学习经验.求挑选的两人恰好分别来自A、B两组的概率.
| 使用智能手机人数 | 不使用智能手机人数 | 合计 | |
| 学习成绩优秀人数 | 4 | 8 | 12 |
| 学习成绩不优秀人数 | 16 | 2 | 18 |
| 合计 | 20 | 10 | 30 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(Ⅰ)试根据以上数据,运用独立性检验思想,指出有多大把握认为中学生使用智能手机对学习有影响?
(Ⅱ)研究小组将该样本中使用智能手机且成绩优秀的4位同学记为A组,不使用智能手机且成绩优秀的8位同学记为B组,计划从A组推选的2人和B组推选的3人中,随机挑选两人在学校升旗仪式上作“国旗下讲话”分享学习经验.求挑选的两人恰好分别来自A、B两组的概率.
13.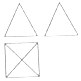 某四棱锥的三视图如图所示,正视图、侧视图都是边长为$2\sqrt{3}$的等边三角形,俯视图是一个正方形,则此四棱锥的体积是( )
某四棱锥的三视图如图所示,正视图、侧视图都是边长为$2\sqrt{3}$的等边三角形,俯视图是一个正方形,则此四棱锥的体积是( )
 某四棱锥的三视图如图所示,正视图、侧视图都是边长为$2\sqrt{3}$的等边三角形,俯视图是一个正方形,则此四棱锥的体积是( )
某四棱锥的三视图如图所示,正视图、侧视图都是边长为$2\sqrt{3}$的等边三角形,俯视图是一个正方形,则此四棱锥的体积是( )| A. | $8\sqrt{3}$ | B. | 12 | C. | 24 | D. | 36 |
10.设公比为q(q>0)的等比数列{an}的前项和为Sn,若S2=3a2+2,S4=3a4+2,则a1=( )
| A. | -2 | B. | -1 | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
7.若${({\frac{3}{{\sqrt{x}}}-\root{3}{x}})^n}$的展开式中所有项系数的绝对值之和为1024,则该展开式中的常数项是( )
| A. | -270 | B. | 270 | C. | -90 | D. | 90 |
8.对于函数f(x)=atanx+bx3+cx(a、b、c∈R),选取a、b、c的一组值计算f(1)、f(-1),所得出的正确结果可能是( )
| A. | 2和1 | B. | 2和0 | C. | 2和-1 | D. | 2和-2 |