题目内容
3．下列命题推断错误的是（ ）| A． | 命题“若x=y，则sinx=siny”的逆否命题为真命题 | |
| B． | 若p且q为假命题，则p，q均为假命题 | |
| C． | “x=-1”是“x2-5x-6=0”的充分不必要条件 | |
| D． | 命题p：存在x0∈R，使得x02+x0+1＜0，则非p：任意x∈R，都有x2+x+1≥0 |
分析 利用原命题与逆否命题的真假关系判断A的正误；复合命题的真假判断B的正误；充要条件判断C的正误；命题的否定判断D的正误；
解答 解：对于A，命题“若x=y，则sinx=siny”是真命题，它的逆否命题为真命题，所以A正确；
对于B，若p且q为假命题，则p，q均为假命题，只要一个命题是假命题，命题就是假命题，所以B不正确；
对于C，“x=-1”是“x2-5x-6=0”的充分不必要条件，满足充要条件，正确；
对于D，命题p：存在x0∈R，使得$x_0^2+{x_0}+1＜0$，则非p：任意x∈R，都有$x_{\;}^2+{x_{\;}}+1≥0$．满足命题的否定形式，正确；
故选：B．
点评 本题考查命题的真假的判断与应用，充要条件，命题的否定，四种命题的逆否关系，基本知识的考查．
练习册系列答案
相关题目
13．
某四棱锥的三视图如图所示，正视图、侧视图都是边长为$2\sqrt{3}$的等边三角形，俯视图是一个正方形，则此四棱锥的体积是（ ）
某四棱锥的三视图如图所示，正视图、侧视图都是边长为$2\sqrt{3}$的等边三角形，俯视图是一个正方形，则此四棱锥的体积是（ ）| A． | $8\sqrt{3}$ | B． | 12 | C． | 24 | D． | 36 |
8．对于函数f（x）=atanx+bx3+cx（a、b、c∈R），选取a、b、c的一组值计算f（1）、f（-1），所得出的正确结果可能是（ ）
| A． | 2和1 | B． | 2和0 | C． | 2和-1 | D． | 2和-2 |
15．已知f（x），g（x）都是定义在R上的函数，g（x）≠0，f（x）g′（x）＞f′（x）g（x），f（x）=ax•g（x）（a＞0，a≠1），$\frac{f（1）}{g（1）}+\frac{f（-1）}{g（-1）}=\frac{5}{2}$，在有穷数列$\{\frac{f（n）}{g（n）}\}$（n=1，2…10）中，任意取正整数k（1≤k≤10），则前k项和大于$\frac{15}{16}$的概率是（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
12．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的一个焦点与抛物线${y^2}=4\sqrt{3}x$的焦点重合，长轴长等于圆x2+y2-2x-15=0的半径，则椭圆C的方程为（ ）
| A． | $\frac{x^2}{4}+\frac{y^2}{3}=1$ | B． | $\frac{x^2}{16}+\frac{y^2}{12}=1$ | C． | $\frac{x^2}{4}+{y^2}=1$ | D． | $\frac{x^2}{16}+\frac{y^2}{4}=1$ |
13．
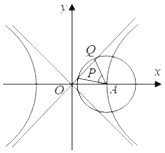如图，已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的右顶点为A，O 为坐标原点，以A 为圆心的圆与双曲线C 的一条渐近线交于 P，Q 两点．若∠PAQ=60°，且|PQ|=$\frac{{\sqrt{3}}}{3}a$，则双曲线C 的渐近线方程为（ ）
如图，已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的右顶点为A，O 为坐标原点，以A 为圆心的圆与双曲线C 的一条渐近线交于 P，Q 两点．若∠PAQ=60°，且|PQ|=$\frac{{\sqrt{3}}}{3}a$，则双曲线C 的渐近线方程为（ ）| A． | $y=±\frac{{\sqrt{3}}}{3}x$ | B． | $y=±\frac{{\sqrt{3}}}{2}x$ | C． | y=±3x | D． | $y=±\frac{{2\sqrt{3}}}{3}x$ |