题目内容
19.已知A,B,C三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如表(单位:小时).| A 班 | 6 | 6.5 | 7 | |
| B 班 | 6 | 7 | 8 | |
| C 班 | 5 | 6 | 7 | 8 |
(2)从A班和B班抽出来的学生中各选一名,记A班选出的学生为甲,B班选出的学生为乙,求甲的锻炼时间大于乙的锻炼时间的概率.
分析 (1)由已知先计算出抽样比,进而可估计C班的学生人数;
(2)根据古典概型概率计算公式,可求出该周甲的锻炼时间比乙的锻炼时间长的概率.
解答 解:(1)由分层抽样可得C班人数为:$100×\frac{4}{3+3+4}=40$(人);
(2)记从A班选出学生锻炼时间为x,B班选出学生锻炼时间为y,则所有(x,y)为(6,6),(6,7),(6,8),(6.5,6),(6.5,7),(6.5,8),(7,6),(7,7),(7,8)共9种情况,而满足x>y的(6.5,6),(7,6)有2种情况,所以,所求概率$P=\frac{2}{9}$.
点评 本题考查的知识点是用样本的频率分布估计总体分布,古典概型,难度中档.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
9.$\int_{\frac{π}{2}}^π{sinx}dx$的值为( )
| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{1}{2}$ | D. | 1 |
14.长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=2$\sqrt{2}$,则长方体ABCD-A1B1C1D1的外接球的表面积为( )
| A. | 36π | B. | 28π | C. | 16π | D. | 12π |
4.命题?x>0,ln(x+1)>0的否定为( )
| A. | ?x0<0,ln(x0+1)<0 | B. | ?x0≤0,ln(x0+1)≤0 | C. | ?x0>0,ln(x0+1)<0 | D. | ?x0>0,ln(x0+1)≤0 |
13.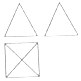 某四棱锥的三视图如图所示,正视图、侧视图都是边长为$2\sqrt{3}$的等边三角形,俯视图是一个正方形,则此四棱锥的体积是( )
某四棱锥的三视图如图所示,正视图、侧视图都是边长为$2\sqrt{3}$的等边三角形,俯视图是一个正方形,则此四棱锥的体积是( )
 某四棱锥的三视图如图所示,正视图、侧视图都是边长为$2\sqrt{3}$的等边三角形,俯视图是一个正方形,则此四棱锥的体积是( )
某四棱锥的三视图如图所示,正视图、侧视图都是边长为$2\sqrt{3}$的等边三角形,俯视图是一个正方形,则此四棱锥的体积是( )| A. | $8\sqrt{3}$ | B. | 12 | C. | 24 | D. | 36 |
 如图,在△ABC中,边BC上的高所在的直线方程为x-3y+2=0,∠BAC的平分线所在的直线方程为y=0,若点B的坐标为(1,3).
如图,在△ABC中,边BC上的高所在的直线方程为x-3y+2=0,∠BAC的平分线所在的直线方程为y=0,若点B的坐标为(1,3).