题目内容
20.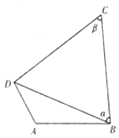 如图,在圆内接四边形ABCD中,AB=2,AD=1,$\sqrt{3}$BC=$\sqrt{3}$BDcosα+CDsinβ
如图,在圆内接四边形ABCD中,AB=2,AD=1,$\sqrt{3}$BC=$\sqrt{3}$BDcosα+CDsinβ(Ⅰ)求角β的大小
(Ⅱ)求四边形ABCD周长的取值范围.
分析 (Ⅰ)条件化为$\sqrt{3}$sin(α+β)=$\sqrt{3}$sinβcosα+sinαsinβ,即可求角β的大小
(Ⅱ)求出CB+CD$≤2\sqrt{7}$,即可求四边形ABCD周长的取值范围.
解答 解:(Ⅰ)∵$\sqrt{3}$BC=$\sqrt{3}$BDcosα+CDsinβ,
∴$\sqrt{3}$sin∠BDC=$\sqrt{3}$sinβcosα+sinαsinβ,
∴$\sqrt{3}$sin(α+β)=$\sqrt{3}$sinβcosα+sinαsinβ,
化简可得tanβ=$\sqrt{3}$,∴β=$\frac{π}{3}$;
(Ⅱ)由题意,$∠BAD=\frac{2π}{3}$,BD=$\sqrt{4+1-2×2×1×(-\frac{1}{2})}$=$\sqrt{7}$,
∵BD2=CB2+CD2-2CB•CD•cosβ=(CB+CD)2-3CB•CD≥$\frac{(CB+CD)^{2}}{4}$,
∴CB+CD$≤2\sqrt{7}$,
∵$CB+CD>\sqrt{7}$,
∴四边形ABCD周长的取值范围(3+$\sqrt{7}$,3+2$\sqrt{7}$).
点评 本题考查三角函数的化简,考查余弦定理的运用,属于中档题.

练习册系列答案
相关题目
1.双曲线$\frac{{x}^{2}}{4}$$-\frac{{y}^{2}}{3}$=1的焦点到渐近线的距离为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{2}$ |
11.直线x-y+1=0的倾斜角为( )
| A. | 90° | B. | 45° | C. | 135° | D. | 60° |
8.某三棱锥的三视图如图所示,则俯视图的面积为( )


| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | 4 |
15. 某几何体的三视图如图所示,则其体积为( )
某几何体的三视图如图所示,则其体积为( )
 某几何体的三视图如图所示,则其体积为( )
某几何体的三视图如图所示,则其体积为( )| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
5.函数f(x)=$\left\{\begin{array}{l}{-x-4,(x<0)}\\{{x}^{2}-4,(x>0)}\end{array}\right.$的零点为( )
| A. | -4或-2 | B. | -4或2 | C. | -2或4 | D. | -2或2 |
12.抛物线y=$\frac{1}{8}$x2的焦点坐标为( )
| A. | ($\frac{1}{32}$,0) | B. | (0,$\frac{1}{32}$) | C. | (0,4) | D. | (0,2) |
9.已知一组样本数据(xi,yi)如表
设其线性回归方程$\widehat{y}$=bx+a,若已求出b=0.7,则线性回归方程为( )
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
| A. | $\widehat{y}$=0.7x+0.35 | B. | $\widehat{y}$=0.7x+4.5 | C. | $\widehat{y}$=0.7x-0.35 | D. | $\widehat{y}$=0.7x-4.5 |