题目内容
若复数z满足
=i3,则z= .
| 1-i |
| z |
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:由已知得z=
=
=1+i.
| 1-i |
| -i |
| i-i2 |
| -i2 |
解答:
解:∵复数z满足
=i3=-i,
∴z=
=
=1+i.
故答案为:1+i.
| 1-i |
| z |
∴z=
| 1-i |
| -i |
| i-i2 |
| -i2 |
故答案为:1+i.
点评:本题考查复数的求法,是基础题,解题时要注意复数的乘除运算法则的合理运用.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
命题“x2-9=0的解是x=±3”,在这个命题中,使用的逻辑联结词的情况是( )
| A、没有使用逻辑联结词 |
| B、使用了“且” |
| C、使用了“或” |
| D、使用了“非” |
用数学归纳法证明等式(n+1)(n+2)×…×(n+n)=2n×1×3×…×(2n-1)的过程中,由n=k(k∈N*)推出n=k+1(k∈N*)成立时,左边应增加的因式是( )
| A、2k+1 | ||
| B、2(2k+1) | ||
C、
| ||
D、
|
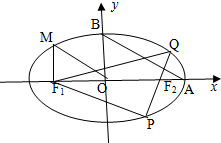 如图,从椭圆
如图,从椭圆 如图所示,已知A,B均为集合U={1,2,5,7,11}的子集,且A∩B={2},(∁UB)∩A={11},则集合A等于
如图所示,已知A,B均为集合U={1,2,5,7,11}的子集,且A∩B={2},(∁UB)∩A={11},则集合A等于