题目内容
已知函数f(x)=(
)|x-1|+a|x+2|.当a=1时,f(x)的单调递减区间为 ;当a=-1时,f(x)的单调递增区间为 .
| 1 |
| 2 |
考点:函数的单调性及单调区间
专题:函数的性质及应用
分析:(1)当a=1时,f(x)=(
)|x-1|+|x+2|,令u(x)=|x-1|+|x+2|=
,利用复合函数的单调性判断即可,
(2)当a=-1时,f(x)=(
)|x-1|-|x+2|令u(x)=|x-1|-|x+2|=
,根据复合函数的单调性可判断即可.
| 1 |
| 2 |
|
(2)当a=-1时,f(x)=(
| 1 |
| 2 |
|
解答:
解:(1)∵f(x)=(
)|x-1|+a|x+2|.
∴当a=1时,f(x)=(
)|x-1|+|x+2|,
令u(x)=|x-1|+|x+2|=
,
∴u(x)在[1,+∞)单调递增,
根据复合函数的单调性可判断:f(x)的单调递减区间为[1,+∞),
(2)当a=-1时,f(x)=(
)|x-1|-|x+2|
令u(x)=|x-1|-|x+2|=
,
u(x)在[-2,1]单调递减,
∴根据复合函数的单调性可判断:f(x)的单调递增区间为[-2,1],
故答案为:[1,+∞),[-2,1],
| 1 |
| 2 |
∴当a=1时,f(x)=(
| 1 |
| 2 |
令u(x)=|x-1|+|x+2|=
|
∴u(x)在[1,+∞)单调递增,
根据复合函数的单调性可判断:f(x)的单调递减区间为[1,+∞),
(2)当a=-1时,f(x)=(
| 1 |
| 2 |
令u(x)=|x-1|-|x+2|=
|
u(x)在[-2,1]单调递减,
∴根据复合函数的单调性可判断:f(x)的单调递增区间为[-2,1],
故答案为:[1,+∞),[-2,1],
点评:本题考查了函数的单调性,复合函数的单调性的判断,属于中档题,关键是去绝对值.

练习册系列答案
相关题目
 已知函数y=Asin(ωx+φ)(A>0,|φ|<π)的一段图象如图所示.
已知函数y=Asin(ωx+φ)(A>0,|φ|<π)的一段图象如图所示.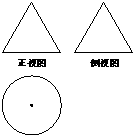 已知某几何体的三视图如图所示,其正视图与侧视图都是边长为2的等边三角形,则该几何体的体积等于
已知某几何体的三视图如图所示,其正视图与侧视图都是边长为2的等边三角形,则该几何体的体积等于