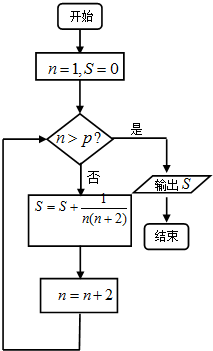
题目内容
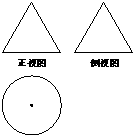 已知某几何体的三视图如图所示,其正视图与侧视图都是边长为2的等边三角形,则该几何体的体积等于
已知某几何体的三视图如图所示,其正视图与侧视图都是边长为2的等边三角形,则该几何体的体积等于考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:该几何体是圆锥,其轴截面为边长为2的等边三角形.即可得出.
解答:
解:该几何体是圆锥,其轴截面为边长为2的等边三角形.
∴该几何体的体积V=
×π×12×
=
.
故答案为:
.
∴该几何体的体积V=
| 1 |
| 3 |
| 3 |
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题考查了圆锥的三视图及其体积计算公式,属于基础题.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目
先把函数f(x)=sin(x-
)的图象上各点的横坐标变为原来的
倍(纵坐标不变),再把新得到的图象向右平移
个单位,得到y=g(x)的图象.当x∈(
,
))时,函数g(x)的值域为( )
| π |
| 6 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 4 |
| 3π |
| 4 |
A、(-
| ||||||||
B、(-
| ||||||||
C、(-
| ||||||||
| D、[-1,0) |
设全集U=R,A={x|y=ln(1-x)},B={x||x-1|<1},则(∁UA)∩B=( )
| A、(-2,1) |
| B、(-2,1] |
| C、[1,2) |
| D、(1,2) |
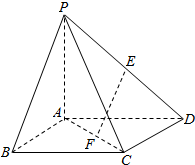 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E、F分别为PD、AC上的动点,且
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E、F分别为PD、AC上的动点,且