题目内容
已知函数f(x)=2cosxsin(x+
)-
.
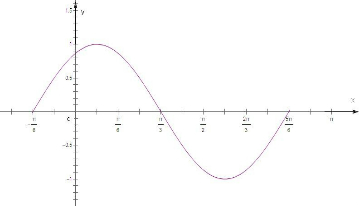
(1)用“五点作图法”画出函数f(x)在一个周期内的图象;
(2)求函数f(x)的单调区间;
(3)求函数f(x)取得最大值和最小值时的集合.
| π |
| 3 |
| ||
| 2 |
(1)用“五点作图法”画出函数f(x)在一个周期内的图象;
(2)求函数f(x)的单调区间;
(3)求函数f(x)取得最大值和最小值时的集合.
考点:五点法作函数y=Asin(ωx+φ)的图象,正弦函数的图象
专题:三角函数的求值,三角函数的图像与性质
分析:(1)先化简求出函数的解析式,然后列表描点即可用“五点作图法”画出函数f(x)在一个周期内的图象;
(2)令2kπ-
≤2x+
≤2kπ+
,k∈Z,令2kπ+
≤2x+
≤2kπ+
,k∈Z,可解得函数f(x)的单调区间;
(3)令2x+
=2kπ+
,k∈Z,2x+
=2kπ+
,k∈Z,从而可求函数f(x)取得最大值和最小值时的集合.
(2)令2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
(3)令2x+
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
解答:
解:(1)f(x)=2cosxsin(x+
)-
=
sin2x+
(1+cos2x)-
=sin(2x+
)
列表:…(6分)
描点、连线如图所示.…(12分)
(2)令2kπ-
≤2x+
≤2kπ+
,k∈Z,可解得kπ-
≤x≤kπ+
,k∈Z,故函数f(x)的单调递增区间是[kπ-
,kπ+
],k∈Z;
令2kπ+
≤2x+
≤2kπ+
,k∈Z,可解得kπ+
≤x≤kπ+
,k∈Z,故函数f(x)的单调递增区间是[kπ+
,kπ+
],k∈Z;
(3)由f(x)max=1,可解得2x+
=2kπ+
,k∈Z,从而有x=kπ+
,k∈Z;
由f(x)min=-1,可解得2x+
=2kπ+
,k∈Z,从而有x=kπ+
,k∈Z.
| π |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| π |
| 3 |
列表:…(6分)
| x | -
|
|
|
|
| ||||||||||
2x+
| 0 |
| π |
| 2π | ||||||||||
| y | 0 | 1 | 0 | -1 | 0 |

(2)令2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
| π |
| 12 |
| 5π |
| 12 |
| π |
| 12 |
令2kπ+
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| π |
| 12 |
| 7π |
| 12 |
| π |
| 12 |
| 7π |
| 12 |
(3)由f(x)max=1,可解得2x+
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
由f(x)min=-1,可解得2x+
| π |
| 3 |
| 3π |
| 2 |
| 7π |
| 12 |
点评:本题主要考查了五点法作函数y=Asin(ωx+φ)的图象,三角函数的图象与性质,属于基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若
=
,
=
,
=λ
(λ≠-1),则
=( )
| OP1 |
| a |
| OP2 |
| b |
| P1P |
| PP2 |
| OP |
A、
| ||||||||
B、λ
| ||||||||
C、λ
| ||||||||
D、
|
已知全集U={x|2≤x≤10,且x∈N}.集合A={3,4,6,8},B={3,5,8,9},那么集合{2,7,10}=( )
| A、A∪B |
| B、A∩B |
| C、(∁UA)∩(∁UB) |
| D、(∁UA)∪(∁UB) |
已知a∈R,则“a>2”是“a2>4”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
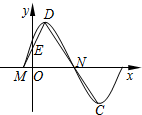 右图为函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<
右图为函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<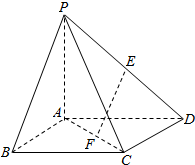 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E、F分别为PD、AC上的动点,且
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E、F分别为PD、AC上的动点,且