题目内容
已知tanα=-2，计算
．
| 3sin2(π-α)-2cos2(π-α)+sin(2π-α)cos(π+α) |
| 1+2sin2α+cos2α |
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：利用三角函数的诱导公式与三角函数间的平方关系式可将所求的关系式化简为原式=
，将tanα=-2代入该式计算即可．
| 3tan2α+tanα-2 |
| 3tan2α+2 |
解答：
解：∵tanα=-2，
∴原式=
=
=
=
=
．
∴原式=
| 3sin2α-2cos2α+(-sinα)•(-cosα) |
| 1+2sin2α+cos2α |
=
| 3sin2α-2cos2α+sinαcosα |
| 3sin2α+2cos2α |
=
| 3tan2α+tanα-2 |
| 3tan2α+2 |
=
| 3×4-2-2 |
| 4×4+2 |
| 4 |
| 9 |
点评：本题考查运用诱导公式化简求值，熟练掌握三角函数的诱导公式与三角函数间的平方关系是化简求值的关键，属于中档题．
练习册系列答案
目标测试系列答案
相关题目
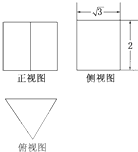如图为一个几何体的三视图，正视图和侧视图均为矩形，俯视图为正三角形，尺寸如图，则该几何体的表面积为（ ）A、14
| ||
B、6+
| ||
C、12+2
| ||
D、16+2
|
已知实数等比数列{an}中，Sn是它的前n项和．若a2•a3=2a1，且a4与2a7的等差中项为
，则S5等于（ ）
| 5 |
| 4 |
| A、35 | B、33 | C、31 | D、29 |
将函数y=sin（x-
）的图象上所有点的横坐标缩短为原来的
（纵坐标不变），再将所得函数的图象向左平移
个单位，则最终所得函数图象对应的解析式为（ ）
| π |
| 6 |
| 1 |
| 2 |
| π |
| 3 |
A、y=cos
| ||
| B、y=sin2x | ||
C、y=sin
| ||
| D、y=cos2x |