题目内容

已知点A（1，-2），B（m，2），且线段AB的垂直平分线的方程是x+2y-2=0，则实数m的值是
 
．
考点：直线的一般式方程与直线的垂直关系
专题：直线与圆
分析：由题意可得点A、B的中点（
1+m
2
，0）在直线x+2y-2=0上，代入可得m的方程，解方程可得m的值．
解答： 解：∵线段AB的垂直平分线的方程是x+2y-2=0，
∴点A、B的中点（
1+m
2
，0）在直线x+2y-2=0上，
∴
1+m
2
+2×0-2=0，解得m=3
故答案为：3．
点评：本题考查直线的一般式方程，涉及中点坐标公式，属基础题．
练习册系列答案
相关题目
求函数y=x2-4|x|-12的单调递减区间．
等比数列{an}的前n项和为Sn，若a1=1，且4a1，2a2，a3成等差数列，则S6=（　　）
A、63B、64C、31D、32
函数f（x）=loga（x2-ax+2）（a＞0，且a≠1）在区间（1，+∞）上恒为正值，则实数a的取值范围为
 
．
已知函数y=b+(a2+1)x2+2x（a，b是常数）在区间[-
3
2
，0]上有ymax=3，ymin=
5
2
，则a2+b2=（　　）
A、2B、10C、8D、5
△ABC中，∠A=90°，AB=2，AC=1，设点P，Q满足
AP
=λ
AB
，
AQ
=（1-λ）
AC
，λ∈R．若
BQ
•
CP
=-2，则λ=（　　）
A、
1
3
B、
2
3
C、
4
3
D、2
垂直于直线x+3y-5=0且经过点P（-1，0）的直线的一般式方程是
 
．
已知tanα=-2，计算
3sin2(π-α)-2cos2(π-α)+sin(2π-α)cos(π+α)
1+2sin2α+cos2α
．
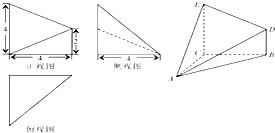已知某几何体的三视图如图所示，其中俯视图和侧视图都是腰长为4的等腰直角三角形，正视图为直角梯形，则此几何体的体积V为（　　）
A、32
B、16
C、
16
3
D、40

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网