题目内容
将函数y=sin(x-
)的图象上所有点的横坐标缩短为原来的
(纵坐标不变),再将所得函数的图象向左平移
个单位,则最终所得函数图象对应的解析式为( )
| π |
| 6 |
| 1 |
| 2 |
| π |
| 3 |
A、y=cos
| ||
| B、y=sin2x | ||
C、y=sin
| ||
| D、y=cos2x |
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:根据三角函数解析式之间的关系即可得到结论.
解答:
解:函数y=sin(x-
)的图象上所有点的横坐标缩短为原来的
(纵坐标不变),得到y=sin(2x-
),
再将所得函数的图象向左平移
个单位,得到y=sin[2(x+
)-
]=sin(2x+
)=cos2x,
故选:D
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
再将所得函数的图象向左平移
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
故选:D
点评:本题主要考查函数解析的求解,根据函数关系和函数解析式之间的关系是解决本题的关键.

练习册系列答案
 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
等比数列{an}的前n项和为Sn,若a1=1,且4a1,2a2,a3成等差数列,则S6=( )
| A、63 | B、64 | C、31 | D、32 |
已知△ABC的三个顶点A(2,4),B(-1,2),C(1,0),点P(x,y)在△ABC的内部及边界运动,则z=x-y( )
| A、在点A处有最大值-2 |
| B、在点B处有最大值-3 |
| C、在点A处有最小值-2 |
| D、在点C处有最大值1 |
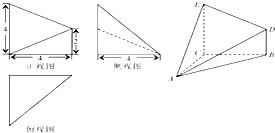 已知某几何体的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,则此几何体的体积V为( )
已知某几何体的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,则此几何体的体积V为( )| A、32 | ||
| B、16 | ||
C、
| ||
| D、40 |
设a>0,b>0.若4a+b=ab,则a+b的最小值是( )
| A、1 | B、5 | C、7 | D、9 |