题目内容
计算机毕业考试分为理论与操作两部分,每部分考试成绩只记“合格”与“不合格”,只有当两部分考试都“合格”者,才颁发计算机“合格证书”.甲、乙两人在理论考试中“合格”的概率依次为
、
,在操作考试中“合格”的概率依次为
、
,所有考试是否合格,相互之间没有影响.则甲、乙进行理论与操作两项考试后,恰有1人获得“合格证书”的概率 .
| 4 |
| 5 |
| 2 |
| 3 |
| 1 |
| 2 |
| 5 |
| 6 |
考点:相互独立事件的概率乘法公式
专题:概率与统计
分析:根据相互独立事件的概率乘法公式求得甲合格而乙不合格的概率,以及乙合格而甲不合格的概率,再把这两个值相加,即得所求.
解答:
解:由题意可得,甲合格而乙不合格的概率为
×
×(1-
×
)=
,
乙合格而甲不合格的概率为
×
×(1-
×
)=
,
∴恰有1人获得“合格证书”的概率为
+
=
,
故答案为:
.
| 4 |
| 5 |
| 1 |
| 2 |
| 2 |
| 3 |
| 5 |
| 6 |
| 8 |
| 45 |
乙合格而甲不合格的概率为
| 2 |
| 3 |
| 5 |
| 6 |
| 4 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
∴恰有1人获得“合格证书”的概率为
| 8 |
| 45 |
| 1 |
| 3 |
| 23 |
| 45 |
故答案为:
| 23 |
| 45 |
点评:本题主要考查相互独立事件的概率乘法公式,所求的事件的概率与它的对立事件的概率之间的关系,属于中档题.

练习册系列答案
相关题目
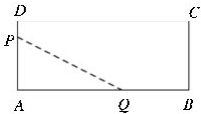 如图,有一矩形地块ABCD,其相邻边长为20m和50m,现要在它的短边与长边上各取一点P与Q,用周长为80m的篱笆围出一块直角三角形的花园,则围出部分的最大面积为
如图,有一矩形地块ABCD,其相邻边长为20m和50m,现要在它的短边与长边上各取一点P与Q,用周长为80m的篱笆围出一块直角三角形的花园,则围出部分的最大面积为