题目内容
5.在区域$Ω=\left\{{(x,y)|\left\{\begin{array}{l}x≥0\\ x+y≤1\\ x-y≤1\end{array}\right.}\right\}$中,若满足ax+y>0的区域面积占Ω面积的$\frac{1}{3}$,则实数a的值是( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{2}{3}$ |
分析 先利用二元一次不等式(组)与平面区域,根据约束条件画出可行域,然后求出区域的面积即可,利用目标函数的几何意义,利用数形结合确定a的值
解答 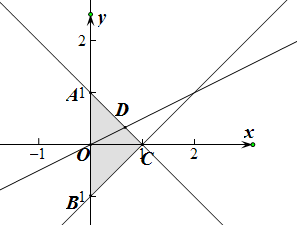 解:作出不等式组对应的平面区域如图:(阴影部分)
解:作出不等式组对应的平面区域如图:(阴影部分)
可知A(0,1),B(0,-1),C(1,0),x,y满足约束条件,
则点P(x,y)所在区域的面积就是三角形的面积:S△ABC=$\frac{1}{2}$×2×1=1.
设y=-ax,
结合图形可知a<0时,才能满足满足ax+y>0的区域面积占Ω面积的$\frac{1}{3}$,
由$\left\{\begin{array}{l}{y=-ax}\\{x+y=1}\end{array}\right.$,解得xD=$\frac{1}{1-a}$,
则S△OAD=$\frac{1}{2}$×1×$\frac{1}{1-a}$=$\frac{1}{3}$,
解得a=-$\frac{1}{2}$,
故选:C.
点评 本题考查线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
16.复数${({1+i})^2}+\frac{2}{1+i}$的共轭复数的虚部是( )
| A. | i | B. | -i | C. | -1 | D. | 1 |
13.已知集合A={x|0<x<2},集合B={x|-1<x<1},集合C={x|mx+1>0},若A∪B⊆C,则实数m的取值范围为( )
| A. | {m|-2≤m≤1} | B. | {m|-$\frac{1}{2}$≤m≤1} | C. | {m|-1≤m≤$\frac{1}{2}$} | D. | {m|-$\frac{1}{2}$≤m≤$\frac{1}{4}$} |
20.已知i是虚数单位,则复数$\frac{-1+i}{3+4i}$的共轭复数在复平面内对应的点所在的象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
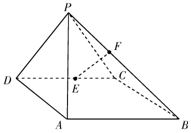 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,$AB=DP=2\sqrt{2}$,E为CD的中点,点F在线段PB上.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,$AB=DP=2\sqrt{2}$,E为CD的中点,点F在线段PB上.