题目内容
已知函数f(x)=Asin(ωx+Φ)(A>0,ω>0,0<Φ<
)图象的最高点M(
,3),且f(x)的最小正周期为π.
(1)求f(x)的解析式;
(2)若函数g(x)=f(
+
),α,β∈(0,π),且g(α)=1,g(β)=
,求g(α+β)的值.
| π |
| 2 |
| π |
| 12 |
(1)求f(x)的解析式;
(2)若函数g(x)=f(
| x |
| 2 |
| π |
| 12 |
| 3 |
| 4 |
| 2 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的图象
专题:计算题,三角函数的求值
分析:(1)由题意即周期公式可得ω的值,由图象的最高点M(
,3),可得A=3,有3sin(2×
+Φ)=3,从而可解得Φ的值,即可求得f(x)的解析式.
(2)由题意可得g(x)=3cosx,从而可求cosα,cosβ,由α,β∈(0,π),可得sinα,sinβ即可求得g(α+β)的值.
| π |
| 12 |
| π |
| 12 |
(2)由题意可得g(x)=3cosx,从而可求cosα,cosβ,由α,β∈(0,π),可得sinα,sinβ即可求得g(α+β)的值.
解答:
解:(1)∵f(x)的最小正周期为π.
∴ω=
=
=2,
∵图象的最高点M(
,3),
∴A=3,
∴有3sin(2×
+Φ)=3,
∴可解得:
+Φ=2kπ+
,k∈Z,可得Φ=2kπ+
,k∈Z,
∵0<Φ<
,
∴Φ=
,
∴f(x)的解析式是:f(x)=3sin(2x+
).
(2)∵g(x)=f(
+
)=3sin[2(
+
)+
]=3sin(x+
)=3cosx.
∴g(α)=3cosα=1,可得:cosα=
,g(β)=3cosβ=
,可得:cosβ=
∵α,β∈(0,π),
∴sinα=
=
,sinβ=
=
∴g(α+β)=3cos(α+β)=3(cosαcosβ-sinαsinβ)=3×
×
-3×
×
=
-
∴ω=
| 2π |
| T |
| 2π |
| π |
∵图象的最高点M(
| π |
| 12 |
∴A=3,
∴有3sin(2×
| π |
| 12 |
∴可解得:
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
∵0<Φ<
| π |
| 2 |
∴Φ=
| π |
| 3 |
∴f(x)的解析式是:f(x)=3sin(2x+
| π |
| 3 |
(2)∵g(x)=f(
| x |
| 2 |
| π |
| 12 |
| x |
| 2 |
| π |
| 12 |
| π |
| 3 |
| π |
| 2 |
∴g(α)=3cosα=1,可得:cosα=
| 1 |
| 3 |
| 3 |
| 4 |
| 2 |
| ||
| 4 |
∵α,β∈(0,π),
∴sinα=
| 1-cos2α |
2
| ||
| 3 |
| 1-cos2β |
| ||
| 4 |
∴g(α+β)=3cos(α+β)=3(cosαcosβ-sinαsinβ)=3×
| 1 |
| 3 |
| ||
| 4 |
2
| ||
| 3 |
| ||
| 4 |
| ||
| 4 |
| 7 |
点评:本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,同角三角函数关系式,两角和的余弦公式的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在等分区间的情况下,f(x)=
(x∈[0,2])及x轴所围成的曲边梯形的面积和式的极限形式正确的是( )
| 1 |
| 1+x2 |
A、
| |||||||||||
B、
| |||||||||||
C、
| |||||||||||
D、
|
已知a>1,e=2.71828…是自然对数的底数,若函数y=logax与y=ax的图象与直线y=x相切于同一点,则a=( )
| A、ee | ||
| B、e2 | ||
| C、e | ||
D、e
|
函数y=log2x的反函数是( )
| A、y=-log2x |
| B、y=x2 |
| C、y=2x |
| D、y=logx2 |
若k∈R,则“-3<k<3”是“方程
-
=1表示双曲线”的( )
| x2 |
| k-3 |
| y2 |
| k+3 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
“m=3”是“椭圆
+
=1的离心率为
”的( )
| x2 |
| 4 |
| y2 |
| m |
| 1 |
| 2 |
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |

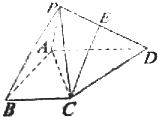 如图所示,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC=
如图所示,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC=