题目内容
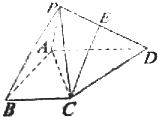 如图所示,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC=
如图所示,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC=| 1 |
| 2 |
(1)求证:平面PAC⊥平面PCD;
(2)在棱PD上是否存在一点E,使CE∥平面PAB?若存在,请确定E点的位置;若不存在,请说明理由.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)设PA=1,由勾股定理逆定理得AC⊥CD,根据线面垂直的性质可知PA⊥CD,又PA∩AC=A,根据线面垂直的判定定理可知CD⊥面PAC,而CD?面PCD,根据面面垂直的判定定理可知面PAD⊥面PCD;
(2)作CF∥AB交于AD于F,作EF∥AP交于PD于E,连接CE,根据面面平行的性质定理可知平面EFC∥平面PAB,又CE?平面EFC,根据面面平行的性质可知CE∥平面PAB,根据线面关系可知E为PD中点,使CE∥面PAB.
(2)作CF∥AB交于AD于F,作EF∥AP交于PD于E,连接CE,根据面面平行的性质定理可知平面EFC∥平面PAB,又CE?平面EFC,根据面面平行的性质可知CE∥平面PAB,根据线面关系可知E为PD中点,使CE∥面PAB.
解答:
解:(1)设PA=1.
由题意PA=BC=1,AD=2.(2分)
∵AB=1,BC=
AD,由∠ABC=∠BAD=90°,得CD=AC=
.
由勾股定理逆定理得AC⊥CD.(3分)
又∵PA⊥面ABCD,CD?面ABCD,
∴PA⊥CD.又PA∩AC=A,∴CD⊥面PAC.(5分)
又CD?面PCD,∴面PAC⊥面PCD.(6分)
(2)作CF∥AB交于AD于F,作EF∥AP交于PD于E,连接CE.(8分)
∵CF∥AB,EF∥PA,CF∩EF=F,PA∩AB=A,
∴平面EFC∥平面PAB.(10分)
又CE?平面EFC,∴CE∥平面PAB.
∵BC=
AD,AF=BC,
∴F为AD的中点,∴E为PD中点.
故棱PD上存在点E,且E为PD中点,使CE∥面PAB.(12分)

由题意PA=BC=1,AD=2.(2分)
∵AB=1,BC=
| 1 |
| 2 |
| 2 |
由勾股定理逆定理得AC⊥CD.(3分)
又∵PA⊥面ABCD,CD?面ABCD,
∴PA⊥CD.又PA∩AC=A,∴CD⊥面PAC.(5分)
又CD?面PCD,∴面PAC⊥面PCD.(6分)
(2)作CF∥AB交于AD于F,作EF∥AP交于PD于E,连接CE.(8分)
∵CF∥AB,EF∥PA,CF∩EF=F,PA∩AB=A,
∴平面EFC∥平面PAB.(10分)
又CE?平面EFC,∴CE∥平面PAB.
∵BC=
| 1 |
| 2 |
∴F为AD的中点,∴E为PD中点.
故棱PD上存在点E,且E为PD中点,使CE∥面PAB.(12分)
点评:本小题主要考查空间中的线面关系,考查线面平行、面面垂直的判定,考查空间想象能力和推理论证能力,考查转化思想,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知向量
=(1,2),2
+
=(3,2),则( )
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
直线x+y-3=0的倾斜角是( )
| A、30° | B、45° |
| C、135° | D、150° |
设z的共轭复数是
,且z+
=4,z•
=8,则
等于( )
. |
| z |
. |
| z |
. |
| z |
| ||
| z |
| A、±1 | B、±i | C、1 | D、-i |