题目内容
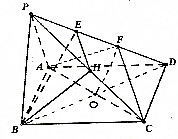如图所示，在四棱锥P-ABCD中，地面四边形ABCD是平行四边形，E、F是棱PD的三等分点，H为棱PC的中点．（1）求证：BE∥平面ACF；
（2）若直线PA交平面BHE与点G，求证：AF∥GE．
考点：直线与平面平行的判定,直线与平面平行的性质
专题：空间位置关系与距离
分析：（1）根据线面平行的判定定理，只要证明BE∥OF即可；
（2）容易得到EH∥FC，结合（1），利用面面平行的判定定理得到平面ACF∥平面BHE，再由面面平行的性质得证．
（2）容易得到EH∥FC，结合（1），利用面面平行的判定定理得到平面ACF∥平面BHE，再由面面平行的性质得证．
解答：
证明：（1）∵底面四边形ABCD是平行四边形，E、F是棱PD的三等分点，H为棱PC的中点．
∴O是BD的中点，F是DE的中点，
∴OF∥BE，
又BE?平面ACF，OF?平面ACF，
∴BE∥平面ACF．
（2）由（1）可知BE∥平面ACF．又EH∥CF，并且BE∩EH=E，AF∩CF=F，
∴平面ACF∥平面BHE，
又平面ACF∩平面PAD=GE，平面BHE∩平面PAD=AF，
∴GE∥AF．
∴O是BD的中点，F是DE的中点，
∴OF∥BE，
又BE?平面ACF，OF?平面ACF，
∴BE∥平面ACF．
（2）由（1）可知BE∥平面ACF．又EH∥CF，并且BE∩EH=E，AF∩CF=F，
∴平面ACF∥平面BHE，
又平面ACF∩平面PAD=GE，平面BHE∩平面PAD=AF，
∴GE∥AF．
点评：本题考查了线面平行的判定定理和性质定理的运用以及面面平行的性质的运用，属于基础题．
练习册系列答案
相关题目
已知非零向量
，
满足|
|=3|
|，且关于x的函数f（x）=
x3+
|
|x2+
•
x为R上增函数，则
，
夹角的取值范围是（ ）
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| a |
| b |
| a |
| b |
A、[0，
| ||||
B、[0，
| ||||
C、（
| ||||
D、（
|
等比数列{an}中，前n项的和为Sn，已知a3=
，S3=
，则S6等于（ ）
| 3 |
| 2 |
| 9 |
| 2 |
A、
| ||
B、9或
| ||
C、
| ||
D、9或
|
已知△ABC的三个内角为A、B、C满足sin2（A+C）＞sin2A+sin2C，则△ABC的形状是（ ）
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、不能确定 |