题目内容
设抛物线y2=4x的焦点为F，准线为l，P为抛物线上一点，PA⊥l，A为垂足，如果直线AF的斜率为
，那么|PF|=（ ）
| 3 |
A、4
| ||
| B、4 | ||
C、8
| ||
| D、8 |
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：求出直线AF的方程，求出点A和P的坐标，利用抛物线的定义即可求|PF|的值．
解答：
解：∵抛物线方程为y2=4x，
∴焦点F（1，0），准线l方程为x=-1，
∵直线AF的斜率为
，
直线AF的方程为y=
（x-1），
当x=-1时，y=2
，
由可得A点坐标为（-1，2
）
∵PA⊥l，A为垂足，
∴P点纵坐标为2
，代入抛物线方程，得P点坐标为（3，-2
），
∴|PF|=|PA|=3-（-1）=4．
故选：B．
解：∵抛物线方程为y2=4x，∴焦点F（1，0），准线l方程为x=-1，
∵直线AF的斜率为
| 3 |
直线AF的方程为y=
| 3 |
当x=-1时，y=2
| 3 |
由可得A点坐标为（-1，2
| 3 |
∵PA⊥l，A为垂足，
∴P点纵坐标为2
| 3 |
| 3 |
∴|PF|=|PA|=3-（-1）=4．
故选：B．
点评：本题主要考查抛物线的几何性质，定义的应用，以及曲线交点的求法，利用抛物线的定义是解决本题的关键．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
若定义在R上的偶函数f（x）满足f（x+2）=f（x）且x∈[0，1]时，f（x）=x，则方程f（x）=log3|x|的零点个数是（ ）
| A、2个 | B、3个 | C、4个 | D、6个 |
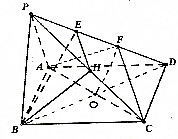如图所示，在四棱锥P-ABCD中，地面四边形ABCD是平行四边形，E、F是棱PD的三等分点，H为棱PC的中点．已知圆锥曲线x2+my2=1的一个焦点坐标为F（
，0），则该圆锥曲线的离心率为（ ）
| 2 | ||
|
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
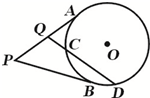已知PA，PB分别为⊙O的两条切线，切点分别为A，B，过PA的中点Q作割线交⊙O于C，D两点，若QC=2，CD=3，则PB=