题目内容
在一次人才招聘会上,有A、B两家公司分别开出它们的工资标准:A公司允诺第一年月工资为1500元,以后每年月工资比上一年月工资增加230元;B公司允诺第一年月工资为2000元,以后每年月工资在上一年的月工资基础上递增5%;设某人年初被A,B两家公司同时录取,试问:
(1)若该人分别在A或B公司连续工作n年,则他在第n年的月工资收入分别是多少;
(2)该人分别在A或B公司连续工作10年,仅从工资收入总量较多作为应聘的标准(不计其他因素),该人应该选择哪家公司,为什么?
(1)若该人分别在A或B公司连续工作n年,则他在第n年的月工资收入分别是多少;
(2)该人分别在A或B公司连续工作10年,仅从工资收入总量较多作为应聘的标准(不计其他因素),该人应该选择哪家公司,为什么?
考点:数列的应用
专题:等差数列与等比数列
分析:(1)设该人在A或B公司连续工作n年,第n年的月收入分别为an,bn,由已知条件能求出an=230n+1270,
bn=2000×1.05n-1.
(2)设该人在A或B公司连续工作10年,工资总收入S,T,分别求出S,T,由此推导出选择A公司.
bn=2000×1.05n-1.
(2)设该人在A或B公司连续工作10年,工资总收入S,T,分别求出S,T,由此推导出选择A公司.
解答:
解:(1)设该人在A或B公司连续工作n年,第n年的月收入分别为an,bn,
∵A公司允诺第一年月工资为1500元,以后每年月工资比上一年月工资增加230元,
B公司允诺第一年月工资为2000元,以后每年月工资在上一年的月工资基础上递增5%,
∴an=230n+1270,
bn=2000×1.05n-1.
(2)设该人在A或B公司连续工作10年,工资总收入S,T,
则S=(1500×10+
×230)×12=304200,
T=
≈301869.
∵S>T,∴选择A公司.
∵A公司允诺第一年月工资为1500元,以后每年月工资比上一年月工资增加230元,
B公司允诺第一年月工资为2000元,以后每年月工资在上一年的月工资基础上递增5%,
∴an=230n+1270,
bn=2000×1.05n-1.
(2)设该人在A或B公司连续工作10年,工资总收入S,T,
则S=(1500×10+
| 10×9 |
| 2 |
T=
| 2000(1-1.0510) |
| 1-1.05 |
∵S>T,∴选择A公司.
点评:本题考查数列在生产、生活中的应用,是中档题,解题时要认真审题,注意等差数列和等比数列的性质的合理运用.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
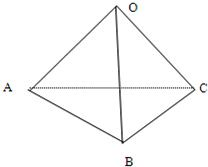 如图所示,已知空间四边形OABC中,OB=|OC|,且∠AOB=∠AOC,则
如图所示,已知空间四边形OABC中,OB=|OC|,且∠AOB=∠AOC,则| OA |
| CB |
| A、0 | ||||
B、
| ||||
C、
| ||||
D、
|
在正方体AC1中,下列关系正确的是( )
| A、A1C1⊥AD |
| B、A1C1⊥BD |
| C、D1C1与AB异面 |
| D、AC1∥DC |
已知等差数列{an}的前n项和为Sn,若a1=1,公差d=2,Sk+1-Sk=13,则k=( )
| A、5 | B、6 | C、7 | D、8 |
 如图所示,在四边形ABCD中,已知A(2,6),B(6,4)、C(5,0)、D(1,0),求直线AC与BD交点P的坐标.
如图所示,在四边形ABCD中,已知A(2,6),B(6,4)、C(5,0)、D(1,0),求直线AC与BD交点P的坐标.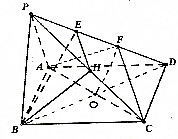 如图所示,在四棱锥P-ABCD中,地面四边形ABCD是平行四边形,E、F是棱PD的三等分点,H为棱PC的中点.
如图所示,在四棱锥P-ABCD中,地面四边形ABCD是平行四边形,E、F是棱PD的三等分点,H为棱PC的中点.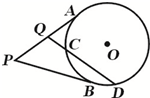 已知PA,PB分别为⊙O的两条切线,切点分别为A,B,过PA的中点Q作割线交⊙O于C,D两点,若QC=2,CD=3,则PB=
已知PA,PB分别为⊙O的两条切线,切点分别为A,B,过PA的中点Q作割线交⊙O于C,D两点,若QC=2,CD=3,则PB=