题目内容
已知非零向量
,
满足|
|=3|
|,且关于x的函数f(x)=
x3+
|
|x2+
•
x为R上增函数,则
,
夹角的取值范围是( )
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| a |
| b |
| a |
| b |
A、[0,
| ||||
B、[0,
| ||||
C、(
| ||||
D、(
|
考点:数量积表示两个向量的夹角,平面向量数量积的运算
专题:函数的性质及应用,导数的综合应用,平面向量及应用
分析:求导数,利用函数f(x)=
x3+
|
|x2+
•
x为R上增函数,可得导数大于或者等于0恒成立,利用判别式小于等于0在R上恒成立,再利用向量的数量积,即可得到结论.
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| a |
| b |
解答:
解:因为于x的函数f(x)=
x3+
|
|x2+
•
x为R上增函数,
所以导数f′(x)=
x2+|
|x+
•
≥0在R上恒成立,
∴△=|
|2-6
•
≤0在R上恒成立,
设
,
夹角为θ,
∵|
|=3|
|≠0,
∴9-18cosθ≤0
∴cosθ≥
,
∵θ∈[0,π]
∴θ∈[0,
]
故选B.
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| a |
| b |
所以导数f′(x)=
| 3 |
| 2 |
| a |
| a |
| b |
∴△=|
| a |
| a |
| b |
设
| a |
| b |
∵|
| a |
| b |
∴9-18cosθ≤0
∴cosθ≥
| 1 |
| 2 |
∵θ∈[0,π]
∴θ∈[0,
| π |
| 3 |
故选B.
点评:本题考查导数知识的运用,考查函数的单调性,考查向量的数量积,解题的关键是利用判别式小于等于0在R上恒成立.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
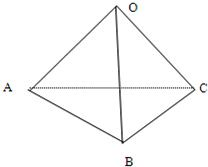 如图所示,已知空间四边形OABC中,OB=|OC|,且∠AOB=∠AOC,则
如图所示,已知空间四边形OABC中,OB=|OC|,且∠AOB=∠AOC,则| OA |
| CB |
| A、0 | ||||
B、
| ||||
C、
| ||||
D、
|
若定义在R上的偶函数f(x)满足f(x+2)=f(x)且x∈[0,1]时,f(x)=x,则方程f(x)=log3|x|的零点个数是( )
| A、2个 | B、3个 | C、4个 | D、6个 |
曲线y=
与直线y=x-1及x=4所围成的封闭图形的面积为( )
| 2 |
| x |
| A、2ln2 |
| B、2-ln2 |
| C、4-ln2 |
| D、4-2ln2 |
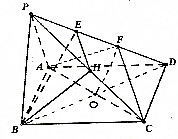 如图所示,在四棱锥P-ABCD中,地面四边形ABCD是平行四边形,E、F是棱PD的三等分点,H为棱PC的中点.
如图所示,在四棱锥P-ABCD中,地面四边形ABCD是平行四边形,E、F是棱PD的三等分点,H为棱PC的中点.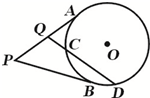 已知PA,PB分别为⊙O的两条切线,切点分别为A,B,过PA的中点Q作割线交⊙O于C,D两点,若QC=2,CD=3,则PB=
已知PA,PB分别为⊙O的两条切线,切点分别为A,B,过PA的中点Q作割线交⊙O于C,D两点,若QC=2,CD=3,则PB=