题目内容
已知△ABC的三个内角为A、B、C满足sin2(A+C)>sin2A+sin2C,则△ABC的形状是( )
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、不能确定 |
考点:三角形的形状判断,正弦定理,余弦定理
专题:解三角形
分析:依题意,利用正弦定理可得b2>a2+c2,再由余弦定理cosB=
<0,可求得B为钝角,从而可得答案.
| a2+c2-b2 |
| 2ac |
解答:
解:△ABC的三个内角为A、B、C满足sin2(A+C)=sin2B>sin2A+sin2C,
∴由正弦定理得:b2>a2+c2,
∴cosB=
<0,B∈(0,π),
∴B为钝角,
∴△ABC的形状是钝角三角形,
故选:C.
∴由正弦定理得:b2>a2+c2,
∴cosB=
| a2+c2-b2 |
| 2ac |
∴B为钝角,
∴△ABC的形状是钝角三角形,
故选:C.
点评:本题考查正弦定理与余弦定理的应用,求得b2>a2+c2是关键,考查转化思想.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
已知等差数列{an}的前n项和为Sn,若a1=1,公差d=2,Sk+1-Sk=13,则k=( )
| A、5 | B、6 | C、7 | D、8 |
曲线y=
与直线y=x-1及x=4所围成的封闭图形的面积为( )
| 2 |
| x |
| A、2ln2 |
| B、2-ln2 |
| C、4-ln2 |
| D、4-2ln2 |
若a>b>0,c>d>0,则一定有( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
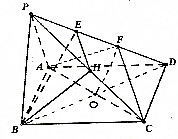 如图所示,在四棱锥P-ABCD中,地面四边形ABCD是平行四边形,E、F是棱PD的三等分点,H为棱PC的中点.
如图所示,在四棱锥P-ABCD中,地面四边形ABCD是平行四边形,E、F是棱PD的三等分点,H为棱PC的中点.