题目内容
9.已知实数a>0,b>0,函数f(x)=ax2+b满足:对任意实数x,y,有f(xy)+f(x+y)≥f(x)f(y),则实数a的取值范围是( )| A. | (0,1] | B. | (0,1) | C. | (0,2) | D. | (0,2] |
分析 令x=y,可得f(x2)+f(2x)≥f2(x),即有ax4+b+4ax2+b≥a2x4+2abx2+b2,即为(a-a2)x4+(4a-2ab)x2+2b-b2≥0,讨论二次项的系数为0和大于0,结合单调性,即可得到所求a的范围.
解答 解:令x=y,可得f(x2)+f(2x)≥f2(x),
即有ax4+b+4ax2+b≥a2x4+2abx2+b2,
即为(a-a2)x4+(4a-2ab)x2+2b-b2≥0,
当a-a2=0,即a=1,(4-2b)x2+2b-b2≥0,
当2-b≥0即b≤2时,不等式恒成立;
当a-a2>0,即0<a<1时,2b-b2≥0,即b≤2,
且-$\frac{4a-2ab}{a-{a}^{2}}$≤0,成立.
综上可得a的范围是(0,1).
故选:B.
点评 本题考查二次函数的单调性的运用,同时考查不等式恒成立问题,注意运用分类讨论的思想方法,属于中档题.

练习册系列答案
相关题目
19.在锐角△ABC中,内角A,B,C的对边分别为a,b,c,若sin2C-cos2C=$\frac{1}{2}$,则下列各式正确的是( )
| A. | a+b=2c | B. | a+b≤2c | C. | a+b<2c | D. | a+b≥2c |
17.已知定义在R上的奇函数f(x),当x>0时,f(x)=-x2-2ax-4.若函数f(x)有5个零点,则实数a的取值范围是( )
| A. | (-∞,-2) | B. | (2,+∞) | C. | (-∞,0) | D. | (-2,2) |
4.已知正项等比数列{an}满足a5+a4-a3-a2=8,则a6+a7的最小值为( )
| A. | 4 | B. | 16 | C. | 24 | D. | 32 |
20.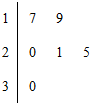 某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则至少有1名优秀工人的概率为
某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则至少有1名优秀工人的概率为
( )
 某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则至少有1名优秀工人的概率为
某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则至少有1名优秀工人的概率为 ( )
| A. | $\frac{8}{15}$ | B. | $\frac{4}{9}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{9}$ |
1.把-1485°转化为α+k•360°(0°≤α<360°,k∈Z)的形式是( )
| A. | 45°-4×360° | B. | -45°-4×360° | C. | -45°-5×360° | D. | 315°-5×360° |
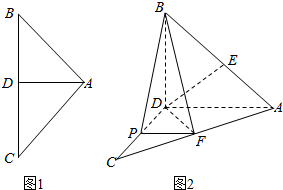 如图1,AD是等腰直角三角形ABC斜边上的高AB=4,沿AD把△ABC的两部分折成直二面角(如图2),P,E,F分别为CD,CA,BA的中点.求证:
如图1,AD是等腰直角三角形ABC斜边上的高AB=4,沿AD把△ABC的两部分折成直二面角(如图2),P,E,F分别为CD,CA,BA的中点.求证: