题目内容
17．已知定义在R上的奇函数f（x），当x＞0时，f（x）=-x2-2ax-4．若函数f（x）有5个零点，则实数a的取值范围是（ ）| A． | （-∞，-2） | B． | （2，+∞） | C． | （-∞，0） | D． | （-2，2） |
分析 由题意可化为f（x）=-x2-2ax-4在（0，+∞）上有两个零点，从而解得．
解答 解：∵f（x）是定义在R上的奇函数，
∴f（0）=0，
∵函数f（x）有5个零点，
∴f（x）在（-∞，0）上有两个零点，
在f（x）=-x2-2ax-4在（0，+∞）上有两个零点，
∴$\left\{\begin{array}{l}{-a＞0}\\{f（0）=-4＜0}\\{f（-a）=-{a}^{2}+2{a}^{2}-4＞0}\end{array}\right.$，
解得，a＜-2，
故选：A．
点评 本题考查了函数的性质的应用及函数的零点的应用，同时考查了二次函数的性质应用．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
8．下列函数中，满足“f（x+y）=f（x）f（y）”的单调递增函数是（ ）
| A． | f（x）=x3 | B． | f（x）=lgx | C． | $f（x）={（{\frac{1}{2}}）^x}$ | D． | f（x）=3x |
9．已知实数a＞0，b＞0，函数f（x）=ax2+b满足：对任意实数x，y，有f（xy）+f（x+y）≥f（x）f（y），则实数a的取值范围是（ ）
| A． | （0，1] | B． | （0，1） | C． | （0，2） | D． | （0，2] |
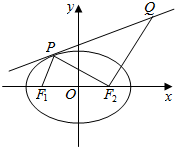已知F1，F2是椭圆$Γ：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左右焦点，椭圆Γ的离心率$e=\frac{{\sqrt{2}}}{2}$，P（x0，y0）是Γ上异于左右顶点的任意一点，且△PF1F2的面积的最大值为1．