题目内容
1．把-1485°转化为α+k•360°（0°≤α＜360°，k∈Z）的形式是（ ）| A． | 45°-4×360° | B． | -45°-4×360° | C． | -45°-5×360° | D． | 315°-5×360° |
分析 根据所给的角是一个负角，用一个360的整倍数的负角，且负角度绝对值比所给的负角度绝对值大，再加上一个周角内的正角，得到结果．
解答 解：-1485°=-1800°+315°=-5×360°+315°，
故选：D
点评 本题看出终边相同的角，本题解题的关键是写出角的大体范围，在看出需要加上多少来平衡角的变化，本题是一个基础题．
练习册系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
9．已知实数a＞0，b＞0，函数f（x）=ax2+b满足：对任意实数x，y，有f（xy）+f（x+y）≥f（x）f（y），则实数a的取值范围是（ ）
| A． | （0，1] | B． | （0，1） | C． | （0，2） | D． | （0，2] |
9．若实数x，y满足$\left\{\begin{array}{l}{2x+y≤8}\\{x+y≥a}\\{x≥0}\end{array}\right.$，且z=60x+20y的最大值为200，则a等于（ ）
| A． | 4 | B． | 6 | C． | 3 | D． | 9 |
16．
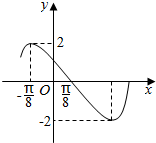已知函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的一段图象如图所示，则函数的解析式为（ ）
已知函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的一段图象如图所示，则函数的解析式为（ ）| A． | y=2sin（2x-$\frac{π}{4}$） | B． | y=2sin（2x-$\frac{π}{4}$）或y=2sin（2x+$\frac{3π}{4}$） | ||
| C． | y=2sin（2x+$\frac{3π}{4}$） | D． | y=2sin（2x-$\frac{3π}{4}$） |
13．x2-ax+b＞0的解集为{x|x＜2或x＞3}，则a+b的值是（ ）
| A． | 1 | B． | -1 | C． | 11 | D． | 12 |
11．已知函数$f（x）=\left\{{\begin{array}{l}{\frac{1}{2}x+1，x≤2}\\{lnx，x＞2}\end{array}}\right.$，方程f（x）-ax=0恰有3个不同实根，则实数a的取值范围是（ ）
| A． | $（\frac{ln2}{2}，\frac{1}{e}）$ | B． | $（0，\frac{1}{2}）$ | C． | $（0，\frac{1}{e}）$ | D． | $（\frac{1}{e}，\frac{1}{2}）$ |