题目内容
19.在锐角△ABC中,内角A,B,C的对边分别为a,b,c,若sin2C-cos2C=$\frac{1}{2}$,则下列各式正确的是( )| A. | a+b=2c | B. | a+b≤2c | C. | a+b<2c | D. | a+b≥2c |
分析 由已知及二倍角公式化简可得cos2C=-$\frac{1}{2}$,解得C=$\frac{π}{3}$.由余弦定理可得c2=b2+a2-ab,可求c2≥ab,又c2+3ab=(b+a)2,推出 (b+a)2≤4c2,即可解得2c≥b+a.
解答 解:∵sin2C-cos2C=$\frac{1}{2}$,
∴cos2C=-$\frac{1}{2}$,解得:C=$\frac{π}{3}$.
∵c2=b2+a2-2ab×cos∠C,即 c2=b2+a2-ab,
∴c2-ab=b2+a2-2ab=(b-a)2≥0,即c2≥ab,
又∵c2=b2+a2+2ab-3ab=(b+a)2-3ab,
即 c2+3ab=(b+a)2,
因为 c2≥ab,推出 (b+a)2≤4c2,
可得:2c≥b+a,
故选:B.
点评 本题主要考查了余弦定理,平方差公式,基本不等式的综合应用,考查了转化思想和计算能力,属于中档题.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
9. 给出以下命题:
给出以下命题:
(1)函数f(x)=$\sqrt{{x}^{2}}$与函数g(x)=|x|是同一个函数;
(2)函数f(x)=ax+1(a>0且a≠1)的图象恒过定点(0,1);
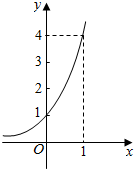
(3)设指数函数f(x)的图象如图所示,若关于x的方程f(x)=$\frac{m-1}{m+1}$有负数根,则实数m的取值范围是(1,+∞);
(4)若f(x)=$\left\{\begin{array}{l}{{2}^{x}+t(x≥0)}\\{g(x)(x<0)}\end{array}\right.$为奇函数,则f(f(-2))=-7;
(5)设集合M={m|函数f(x)=x2-mx+2m的零点为整数,m∈R},则M的所有元素之和为15.
其中所有正确命题的序号为( )
 给出以下命题:
给出以下命题:(1)函数f(x)=$\sqrt{{x}^{2}}$与函数g(x)=|x|是同一个函数;
(2)函数f(x)=ax+1(a>0且a≠1)的图象恒过定点(0,1);
(3)设指数函数f(x)的图象如图所示,若关于x的方程f(x)=$\frac{m-1}{m+1}$有负数根,则实数m的取值范围是(1,+∞);
(4)若f(x)=$\left\{\begin{array}{l}{{2}^{x}+t(x≥0)}\\{g(x)(x<0)}\end{array}\right.$为奇函数,则f(f(-2))=-7;
(5)设集合M={m|函数f(x)=x2-mx+2m的零点为整数,m∈R},则M的所有元素之和为15.
其中所有正确命题的序号为( )
| A. | (1)(2)(3) | B. | (1)(3)(5) | C. | (2)(4)(5) | D. | (1)(3)(4) |
14.若a,b,c∈R,则下列结论中正确的是( )
| A. | 若a>b,则a2>b2 | B. | 若a>b,则ac2>bc2 | C. | 若ac>bc,则a>b | D. | 若a>b,则a-c>b-c |
8.下列函数中,满足“f(x+y)=f(x)f(y)”的单调递增函数是( )
| A. | f(x)=x3 | B. | f(x)=lgx | C. | $f(x)={({\frac{1}{2}})^x}$ | D. | f(x)=3x |
9.已知实数a>0,b>0,函数f(x)=ax2+b满足:对任意实数x,y,有f(xy)+f(x+y)≥f(x)f(y),则实数a的取值范围是( )
| A. | (0,1] | B. | (0,1) | C. | (0,2) | D. | (0,2] |