题目内容
3.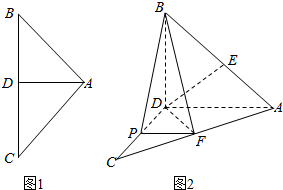 如图1,AD是等腰直角三角形ABC斜边上的高AB=4,沿AD把△ABC的两部分折成直二面角(如图2),P,E,F分别为CD,CA,BA的中点.求证:
如图1,AD是等腰直角三角形ABC斜边上的高AB=4,沿AD把△ABC的两部分折成直二面角(如图2),P,E,F分别为CD,CA,BA的中点.求证:(1)AD∥平面BPF;
(2)求四面体BDFE的体积.
分析 (1)证明AD∥PF,通过直线与平面平行的判定定理证明AD∥面BPF.
(2)通过VBDFEV棱锥B-ADF-V棱锥E-DAF求解几何体的体积即可.
解答  解:(1)证明:∵P,F分别为CD,CA的中点,∴AD∥PF,
解:(1)证明:∵P,F分别为CD,CA的中点,∴AD∥PF,
又因为PF?面BPF,∴AD∥面BPF.
(2)∵AD为高所以AD⊥BD,AD⊥BC,又二面角为直二面角∠BDC为90°,
∴BD⊥DC.
∴BD⊥平面DAF.
VBDFE=V棱锥B-ADF-V棱锥E-DAF=$\frac{1}{3}$S△DAF•BD$-\frac{1}{3}{S}_{△DAF}•\frac{1}{2}BD$=$\frac{2\sqrt{2}}{3}$.
点评 本题考查直线与平面平行的判定定理以及几何体的体积的求法,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
9.已知实数a>0,b>0,函数f(x)=ax2+b满足:对任意实数x,y,有f(xy)+f(x+y)≥f(x)f(y),则实数a的取值范围是( )
| A. | (0,1] | B. | (0,1) | C. | (0,2) | D. | (0,2] |
13.x2-ax+b>0的解集为{x|x<2或x>3},则a+b的值是( )
| A. | 1 | B. | -1 | C. | 11 | D. | 12 |
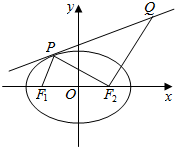 已知F1,F2是椭圆$Γ:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左右焦点,椭圆Γ的离心率$e=\frac{{\sqrt{2}}}{2}$,P(x0,y0)是Γ上异于左右顶点的任意一点,且△PF1F2的面积的最大值为1.
已知F1,F2是椭圆$Γ:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左右焦点,椭圆Γ的离心率$e=\frac{{\sqrt{2}}}{2}$,P(x0,y0)是Γ上异于左右顶点的任意一点,且△PF1F2的面积的最大值为1.