题目内容
1．用二分法求函数f（x）在区间[0，2]上零点的近似解（精确到0.01），若f（0）f（2）＜0，取区间中点x1=1，计算得f（0）f（x1）＜0，则此时可以判定零点x0∈（0，1）（填区间）分析 本题考查的是二分法求函数的近似区间的问题．在解答时，要充分利用条件所给的计算结果，结合二分法的分析规律即可获得问题的解答．
解答 解：由题意可知：对于函数y=f（x）在区间[0，2]上，
有f（0）•f（2）＜0，
利用函数的零点存在性定理，所以函数在（0，2）上有零点．
取区间的中点中点x1=1，
∵计算得f（0）•f（x1）＜0，
∴利用函数的零点存在性定理，函数在（0，1）上有零点．
故答案为：（0，1）．
点评 本题考查的是二分法求函数的近似区间的问题．在解答的过程当中充分体现了二分法解答问题的规律．
练习册系列答案
云南师大附小一线名师提优作业系列答案
相关题目
14．
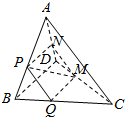如图，在四面体ABCD中，截面PQMN是正方形，且PQ∥AC，则下列命题中，错误的是（ ）
如图，在四面体ABCD中，截面PQMN是正方形，且PQ∥AC，则下列命题中，错误的是（ ）| A． | AC⊥BD | B． | AC∥截面PQMN | ||
| C． | AC=BD | D． | 异面直线PM与BD所成的角为45° |
15．在△ABC中，已知cos（A-B）•cosB-sin（A-B）•sinB=0，则△ABC是（ ）
| A． | 直角三角形 | B． | 等腰三角形 | C． | 等腰直角三角形 | D． | 等边三角形 |
9．在△ABC中，a+b+10c=2（sinA+sinB+10sinC），A=60°，则a=（ ）
| A． | 4 | B． | $\sqrt{3}$ | C． | $2\sqrt{3}$ | D． | 不确定 |
16．设a、b为两条不同的直线，α为一个平面，下列命题中为真命题的是（ ）
| A． | 若a∥b，a∥α，则b∥α | B． | 若a⊥b，a∥α，则b⊥α | C． | 若a∥b，a⊥α，则b⊥α | D． | 若a⊥b，a⊥α，则b∥α |
10．若平面α，β垂直，则下面可以作为这两个平面的法向量的是（ ）
| A． | $\overrightarrow{{n}_{1}}$=（1，2，1），$\overrightarrow{{n}_{2}}$=（-3，1，1） | B． | $\overrightarrow{{n}_{1}}$=（1，1，2），$\overrightarrow{{n}_{2}}$=（-2，1，1） | ||
| C． | $\overrightarrow{{n}_{1}}$=（1，1，1），$\overrightarrow{{n}_{2}}$=（-1，2，1） | D． | $\overrightarrow{{n}_{1}}$=（1，2，1），$\overrightarrow{{n}_{2}}$=（0，-2，-2） |
11．语文、数学、英语共三本课本放成一摞，语文课本与数学课本恰好相邻放置的概率是（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |