题目内容
16.设a、b为两条不同的直线,α为一个平面,下列命题中为真命题的是( )| A. | 若a∥b,a∥α,则b∥α | B. | 若a⊥b,a∥α,则b⊥α | C. | 若a∥b,a⊥α,则b⊥α | D. | 若a⊥b,a⊥α,则b∥α |
分析 根据空间中的平行与垂直的关系即可判断.
解答 解:对于A,若a∥b,a∥α,则b∥α,或b?α,故A错误,
对于B,若a⊥b,a∥α,则b∥α或b?α或b⊥α,故B错误,
对于C,若a∥b,a⊥α,则b⊥α,故正确,
对于D,若a⊥b,a⊥α,则b∥α或b?α,故D错误,
故选:C.
点评 本题通过命题真假的判定,考查了空间中的平行与垂直的关系,属于基础题.

练习册系列答案
相关题目
5.下列说法正确的是( )
| A. | 给定命题p、q,若p∧q是真命题,则¬p是假命题 | |
| B. | 两个三角形全等是这两个三角形面积相等的必要条件 | |
| C. | 命题“?x∈R,x2+x+2013>0”的否定是“?x∈R,x2+x+2013<0” | |
| D. | 函数f(x)=$\frac{1}{x}$在其定义域上是减函数 |
6.已知一次函数f(x)=ax-1满足a∈[-1,2]且a≠0,那么对于a,使得f(x)≤0在x∈[0,1]上成立的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
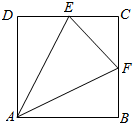 如图,正方形ABCD中,E、F分别为CD、BC的中点,沿AE、AF、EF将其折成一个多面体,则此多面体是直三棱锥.
如图,正方形ABCD中,E、F分别为CD、BC的中点,沿AE、AF、EF将其折成一个多面体,则此多面体是直三棱锥.