题目内容
已知{an}是递增的等差数列，a2，a4是方程x2-5x+6=0的根．
（1）求{an}的通项公式；
（2）求数列{
}的前n项和．
（1）求{an}的通项公式；
（2）求数列{
| an |
| 2n |
考点：数列的求和,等差数列的通项公式
专题：综合题,等差数列与等比数列
分析：（1）解出方程的根，根据数列是递增的求出a2，a4的值，从而解出通项；
（2）将第一问中求得的通项代入，用错位相减法求和．
（2）将第一问中求得的通项代入，用错位相减法求和．
解答：
解：（1）方程x2-5x+6=0的根为2，3．又{an}是递增的等差数列，
故a2=2，a4=3，可得2d=1，d=
，
故an=2+（n-2）×
=
n+1，
（2）设数列{
}的前n项和为Sn，
Sn=
+
+
+…+
+
，①
Sn=
+
+
+…+
+
，②
①-②得
Sn=
+d(
+
+
+…+
)-
=
+
×
-
，
解得Sn=
+
(1-
)-
=2-
．
故a2=2，a4=3，可得2d=1，d=
| 1 |
| 2 |
故an=2+（n-2）×
| 1 |
| 2 |
| 1 |
| 2 |
（2）设数列{
| an |
| 2n |
Sn=
| a1 |
| 21 |
| a2 |
| 22 |
| a3 |
| 23 |
| an-1 |
| 2n-1 |
| an |
| 2n |
| 1 |
| 2 |
| a1 |
| 22 |
| a2 |
| 23 |
| a3 |
| 24 |
| an-1 |
| 2n |
| an |
| 2n+1 |
①-②得
| 1 |
| 2 |
| a1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 2n |
| an |
| 2n+1 |
| ||
| 2 |
| 1 |
| 2 |
| ||||
1-
|
| an |
| 2n+1 |
解得Sn=
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| n+2 |
| 2n+2 |
| n+4 |
| 2n+1 |
点评：本题考查等的性质及错位相减法求和，是近几年高考对数列解答题考查的主要方式．
练习册系列答案
相关题目
设样本数据x1，x2，…，x10的均值和方差分别为1和4，若yi=xi+a（a为非零常数，i=1，2，…，10），则y1，y2，…，y10的均值和方差分别为（ ）
| A、1+a，4 |
| B、1+a，4+a |
| C、1，4 |
| D、1，4+a |
如图，在正方体ABCD-A1B1C1D1中，E、F、P、Q、M、N分别是棱AB、AD、DD1、BB1、A1B1、A1D1的中点，求证：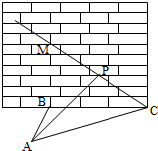
如图，某人在垂直于水平地面ABC的墙面前的点A处进行射击训练．已知点A到墙面的距离为AB，某目标点P沿墙面上的射线CM移动，此人为了准确瞄准目标点P，需计算由点A观察点P的仰角θ的大小．若AB=15m，AC=25m，∠BCM=30°，则tanθ的最大值是