题目内容
已知数列{an}满足anan-1=an-1+(-1)n且a1=1,则
=( )
| a5 |
| a3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:数列递推式
专题:等差数列与等比数列
分析:数列{an}满足anan-1=an-1+(-1)n且a1=1,分别取n=2,3,4,5,即可得出.
解答:
解:∵数列{an}满足anan-1=an-1+(-1)n且a1=1,
∴a2a1=a1+1,解得a2=2,
同理可得:a3=
,a4=3,a5=
.
则
=
.
故选:B.
∴a2a1=a1+1,解得a2=2,
同理可得:a3=
| 1 |
| 2 |
| 2 |
| 3 |
则
| a5 |
| a3 |
| 4 |
| 3 |
故选:B.
点评:本题考查了递推式的应用没看出来计算能力,属于基础题.

练习册系列答案
相关题目
若幂函数f(x)=mxα的图象经过点A(
,
),则它在点A处的切线方程是( )
| 1 |
| 4 |
| 1 |
| 2 |
| A、2x-y=0 |
| B、2x+y=0 |
| C、4x-4y+1=0 |
| D、4x+4y+1=0 |
已知f(x)=
,不等式f(x+a)>f(2a-x)在[a,a+1]上恒成立,则实数a的取值范围是( )
|
| A、(-∞,-2) |
| B、(-∞,0) |
| C、(0,2) |
| D、(-2,0) |
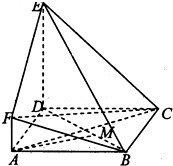 如图,ABCD是正方形,DE⊥平面ABCD.
如图,ABCD是正方形,DE⊥平面ABCD. 在坐标平面内横纵坐标均为整数的点称为格点.现有一只蚂蚁从坐标平面的原点出发,按如下线路沿顺时针方向爬过格点:O→A1(1,0)→A2(1,-1)→A3(0,-1)→A4(-1,-1)→A5(-1,0)→A6(-1,1))→A7(0,1)→A8(1,1)→A9(2,1)→…→A12(2,-2)→…→A16(-2,-2)→…→A20(3,2)→…,则蚂蚁在爬行过程中经过的第350个格点A350坐标为
在坐标平面内横纵坐标均为整数的点称为格点.现有一只蚂蚁从坐标平面的原点出发,按如下线路沿顺时针方向爬过格点:O→A1(1,0)→A2(1,-1)→A3(0,-1)→A4(-1,-1)→A5(-1,0)→A6(-1,1))→A7(0,1)→A8(1,1)→A9(2,1)→…→A12(2,-2)→…→A16(-2,-2)→…→A20(3,2)→…,则蚂蚁在爬行过程中经过的第350个格点A350坐标为