题目内容
己知函数f(x)=x2+bx的图象在点A(1,f(1))处的切线l与直线3x-y=0平行,若数列{
}的前n项和为Sn,则S2015的值为 .
| 1 |
| f(n) |
考点:数列的求和,二次函数的性质
专题:等差数列与等比数列
分析:由已知得f′(1)=2+b=3,从而b=1,进而
=
=
-
,由此得到Sn=
,从而能求出S2015.
| 1 |
| f(n) |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
| n |
| n+1 |
解答:
解:∵函数f(x)=x2+bx的图象在点A(1,f(1))处的切线l与直线3x-y=0平行,
∴f′(x)=2x+b,f′(1)=2+b=3,解得b=1,
∴
=
=
-
,
∴Sn=1-
+
-
+…+
-
=1-
=
,
∴S2015=
.
故答案为:
.
∴f′(x)=2x+b,f′(1)=2+b=3,解得b=1,
∴
| 1 |
| f(n) |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴Sn=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| n |
| n+1 |
∴S2015=
| 2015 |
| 2016 |
故答案为:
| 2015 |
| 2016 |
点评:本题考查数列的前2015项和的求法,是中档题,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
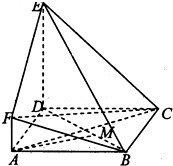 如图,ABCD是正方形,DE⊥平面ABCD.
如图,ABCD是正方形,DE⊥平面ABCD. 在坐标平面内横纵坐标均为整数的点称为格点.现有一只蚂蚁从坐标平面的原点出发,按如下线路沿顺时针方向爬过格点:O→A1(1,0)→A2(1,-1)→A3(0,-1)→A4(-1,-1)→A5(-1,0)→A6(-1,1))→A7(0,1)→A8(1,1)→A9(2,1)→…→A12(2,-2)→…→A16(-2,-2)→…→A20(3,2)→…,则蚂蚁在爬行过程中经过的第350个格点A350坐标为
在坐标平面内横纵坐标均为整数的点称为格点.现有一只蚂蚁从坐标平面的原点出发,按如下线路沿顺时针方向爬过格点:O→A1(1,0)→A2(1,-1)→A3(0,-1)→A4(-1,-1)→A5(-1,0)→A6(-1,1))→A7(0,1)→A8(1,1)→A9(2,1)→…→A12(2,-2)→…→A16(-2,-2)→…→A20(3,2)→…,则蚂蚁在爬行过程中经过的第350个格点A350坐标为