题目内容
在极坐标系中，圆ρ=2cosθ的半径为（ ）
A、
| ||
| B、1 | ||
| C、2 | ||
| D、4 |
考点：简单曲线的极坐标方程
专题：坐标系和参数方程
分析：直接化圆的极坐标方程为直角坐标方程，然后化为标准方程求得圆的半径．
解答：
解：由ρ=2cosθ，得ρ2=2ρcosθ，
化为直角坐标方程得x2+y2=2x，即（x-1）2+y2=1．
∴圆ρ=2cosθ的半径为1．
故选：B．
化为直角坐标方程得x2+y2=2x，即（x-1）2+y2=1．
∴圆ρ=2cosθ的半径为1．
故选：B．
点评：本题考查了简单曲线的极坐标方程，考查了圆的一般方程与标准方程的互化，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知f（x）=
，不等式f（x+a）＞f（2a-x）在[a，a+1]上恒成立，则实数a的取值范围是（ ）
|
| A、（-∞，-2） |
| B、（-∞，0） |
| C、（0，2） |
| D、（-2，0） |
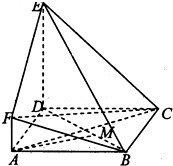如图，ABCD是正方形，DE⊥平面ABCD．
在坐标平面内横纵坐标均为整数的点称为格点．现有一只蚂蚁从坐标平面的原点出发，按如下线路沿顺时针方向爬过格点：O→A1（1，0）→A2（1，-1）→A3（0，-1）→A4（-1，-1）→A5（-1，0）→A6（-1，1））→A7（0，1）→A8（1，1）→A9（2，1）→…→A12（2，-2）→…→A16（-2，-2）→…→A20（3，2）→…，则蚂蚁在爬行过程中经过的第350个格点A350坐标为