题目内容
13.已知a为实数,函数f(x)=(x-a)2+|x-a|-a(a-1).(Ⅰ)若f(0)≤1,求a的取值范围;
(Ⅱ)当a≥2时,讨论f(x)+$\frac{4}{x}$在区间(0,+∞)内零点的个数.
分析 (I)由已知可得f(0)=$\left\{\begin{array}{l}2a,a≥0\\ 0,a<0\end{array}\right.$,若f(0)≤1,则2a≤1,解得:a的取值范围;
(Ⅱ)当a≥2时,f(x)+$\frac{4}{x}$=$\left\{\begin{array}{l}x[x-(2a-1)]+\frac{4}{x},x≥a\\(x-1)(x-2a)+\frac{4}{x},0<x<a\end{array}\right.$,分类讨论,可得f(x)+$\frac{4}{x}$在区间(0,+∞)内零点的个数.
解答 解:(Ⅰ)∵f(x)=(x-a)2+|x-a|-a(a-1).
∴f(0)=a2+|a|-a(a-1)=$\left\{\begin{array}{l}2a,a≥0\\ 0,a<0\end{array}\right.$,
若f(0)≤1,则2a≤1,
解得a$≤\frac{1}{2}$;
(Ⅱ)设F(x)=f(x)+$\frac{4}{x}$=$\left\{\begin{array}{l}x[x-(2a-1)]+\frac{4}{x},x≥a\\(x-1)(x-2a)+\frac{4}{x},0<x<a\end{array}\right.$,
则函数F(x)的图象在区间(0,+∞)上连续,
(1)当a=2时,
①若x≥2,则F(x)=${x}^{2}-3x+\frac{4}{x}$,
F′(x)=2x-3-$\frac{4}{{x}^{2}}$≥0恒成立,即F(x)为增函数,
又由F(2)=0,
故此时f(x)+$\frac{4}{x}$在区间(0,+∞)有且只有一个零点;
②若0<x<2,则F(x)=${x}^{2}-5x+4+\frac{4}{x}$,由${x}^{2}-5x+4>-2,\frac{4}{x}>2$得:
F(x)>0恒成立,
故此时f(x)+$\frac{4}{x}$在区间(0,+∞)没有零点;
(2)当a>2时,
①若x≥a,则F(x)=$x[x-(2a-1)]+\frac{4}{x}$,
F′(x)=2x-(2a-1)-$\frac{4}{{x}^{2}}$>0恒成立,即F(x)为增函数,
②若0<x<a,则F(x)=${x}^{2}-5x+4+\frac{4}{x}$,由${x}^{2}-5x+4>-2,\frac{4}{x}>2$得:
F(x)=2x-(2a+1)-$\frac{4}{{x}^{2}}$<0恒成立,即F(x)为减函数,
又由F(a)=a-a2+$\frac{4}{a}$<0,
故此时f(x)+$\frac{4}{x}$在区间(0,+∞)有两个零点;
综上所述,当a=2时,F(x)有一个零点,a>2时F(x)有两个零点
点评 本题考查的知识点比较多,包括绝对值不等式的解法,函数的零点,函数的导数以及导数与函数的单调性的关系,考查分类讨论思想的应用,函数与方程的思想,转化思想的应用,也考查化归思想的应用.

 阅读快车系列答案
阅读快车系列答案| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
| A. | f(x)在($\frac{1}{2}$,+∞)内是增函数 | B. | f(x)在($\frac{1}{2}$,+∞)内是减函数 | ||
| C. | f(x)在(-∞,$\frac{1}{2}$)内是增函数 | D. | f(x)在(-∞,$\frac{1}{2}$)内是减函数 |
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{5}}{5}$ |

| A. | 1 | B. | e | C. | e2016 | D. | e2017 |
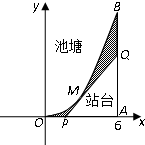 如图,池塘的边缘为曲线段OMB,它可以近似看成是函数f(x)=x2在0≤x≤6的图象,BA垂直于x轴于点A,现要建一个以A为直角的观光站台△APQ,其中斜边PQ与曲线段OMB相切于点M(t,t2),切线PQ交x轴于点P,交线段AB于点Q,图中的阴影部分种植草坪.
如图,池塘的边缘为曲线段OMB,它可以近似看成是函数f(x)=x2在0≤x≤6的图象,BA垂直于x轴于点A,现要建一个以A为直角的观光站台△APQ,其中斜边PQ与曲线段OMB相切于点M(t,t2),切线PQ交x轴于点P,交线段AB于点Q,图中的阴影部分种植草坪. 如图,在三棱柱ABC-A1B1C1中,A1A⊥平面ABC,∠BAC=90°,F为棱AA1上的动点,A1A=4,AB=AC=2.
如图,在三棱柱ABC-A1B1C1中,A1A⊥平面ABC,∠BAC=90°,F为棱AA1上的动点,A1A=4,AB=AC=2.